数据挖掘与大数据分析复习整理

数据挖掘与大数据简介

大纲要求：

• 大数据、数据挖掘、知识发现基本概念

• 数据挖掘产生的原因、数据挖掘的应用

• 数据挖掘的主要功能和数据挖掘面临的挑战

数据挖掘的定义：从大量的数据中挖掘那些令人感兴趣的、有用的、隐含的、先前未知的和可能有用的模式或知识。

注意：并非所有数据分析都是“数据挖掘”：如查询处理、专家系统、或是小型的数学计算/统计程序。

知识发现（ KDD ）的过程

• 数据清理（Data Cleaning）：消除噪声和删除不一致数据。

• 数据集成（Data Integration）：多种数据源可以组合在一起。

• 数据选择（Data Selection）：从数据库中提取与分析任务相关的数据。

• 数据变换（Data Transformation）：把数据变换和统一成适合挖掘的形式。

• 数据挖掘（Data Mining）：核心步骤，使用智能方法提取数据模式。

• 模式评估（Pattern Evaluation）：根据兴趣度度量，识别代表知识的真正有趣的模式。

• 知识表示（Knowledge Representation）：使用可视化和知识表示技术，向用户提供挖掘的知识。

数据挖掘的主要任务

• 关联分析（Association Analysis）
  发现数据之间的关联规则，展示属性/值频繁的在给定的数据中所一起出现的条件。

• 聚类分析（Clustering）
  将类似的数据归类到一起，形成一个新的类别进行分析，最大化类内的相似性和最小化类间的相似性。

• 分类/预测（Classification/Prediction）
  找出描述和区分数据类/概念的模型，使模型能预测未知的对象类标签。

• 孤立点（离群点）分析（Outlier Analysis）
  一些与数据的一般行为或模型不一致的孤立数据，通常被作为“噪音”或异常被丢弃。

大数据时代下数据挖掘的挑战

• 数据容量（ Scale of Data ）：
  新的数据挖掘算法处理大数据，主要集中在新的可扩展算法（采样、哈希、分治等）、Map-reduce 平台（ Hadoop、Spark、GraphLab ）、加速硬件（ GPU/云/集群）。

• 数据实时性（ Data Stream ）：
  处理不断变化的数据流的新数据挖掘算法，主要集中在大规模数据流上的聚类/分类，通过半监督学习处理数据流上的不规则节点/模式挖掘。

• 数据多样性（Different format of data, different sources）：
  为结构化或非结构化数据、不同类型的数据、不同来源的数据等提出新算法，主要集中在不同类型的数据（如，分类数据、名义数据、混合类型数据挖掘）、不同形式的数据（向量数据、图数据、异构数据）、学习不同来源的数据（迁移学习、多任务学习等）、挖掘动态数据（聚类、LBS等）、数据融合或数据集成（多核学习）。

• 数据不确定性（Uncertainty, missing value）：
  不确定性分析、链接/缺失值预测、链接预测（基于聚类、基于结构、基于多视图）、不确定数据聚类（基于概率函数）、推荐系统（缺失项预测等）。

认识数据

• 数据对象：记录、点、向量、模式、事件、样本、案例、观测或实体。

• 属性：刻画对象的基本性质或特性，也称作变量、特性、字段、特征或维。

• 属性值：赋予属性的数或符号（例如，一个人的身高是属性“身高”的属性值）。

• 数据集：数据对象的集合。

属性的类型

• 分类型（Categorical）：

  • 标称（Nominal）：不同的名字，仅提供足够的信息以区分对象（如，眼球颜色）。

  • 序数（Ordinal）：提供足够的信息确定对象的序（如，GPA成绩等级）。

• 数值型（Numerical）：

  • 区间（Interval）：值之间的差是有意义的（如，摄氏温度）。

  • 比率（Ratio）：差和比率都是有意义的（如，开氏温度）。

离散 vs. 连续属性：

• 离散属性（Discrete Attribute）：有限或无限可数个值（如，邮政编码）。

• 连续属性（Continuous Attribute）：属性值为实数（如，温度）。

对称 vs. 非对称属性：

• 对称的二元属性：两个值一样重要（如，性别）。

• 非对称的二元属性：一个值比另一个更重要（如，化验结果中的阳性）。

数据的类型

• 记录数据：数据矩阵、文档数据、购物篮数据（事务数据）。

• 图数据（Graph）：万维网、分子结构。

• 有序数据：时序数据、序列数据、基因序列数据、空间数据。

数据的统计描述

• 中心趋势度量：均值（加权平均、中列数=最大和最小值的平均和）、众数、中位数

  • 大数据背景下，使用线性插值的中位数估计法：确定中位数的上下界$\left\lbrack L_{1},L_{2} \right\rbrack$（宽度为 $W$ ），统计低于下界与在区间内的数据量 $C_{1},C_{2}$，计算中位数估计值：$M = L_{1} + \frac{N/2 - C_{1}}{C_{2}}W$。

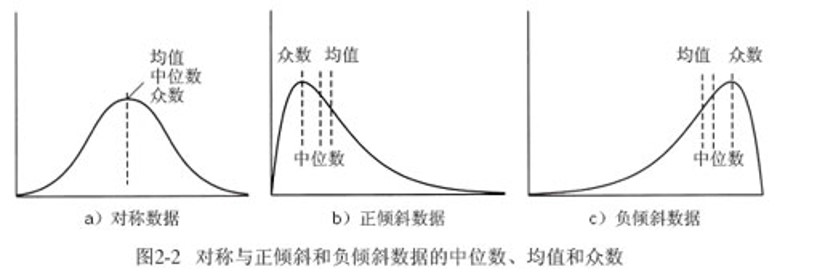
  • 对于非对称的单峰数据,有经验关系：平均数-众数=3(平均数-中位数)。

• 数据的散布：极差、四分位数、四分位数极差=$Q_{3} - Q_{1}$、五数概括 $\left\lbrack \min,Q_{1},\text{ median},Q_{3},\max \right\rbrack$、方差、标准差

• 可视化：分位数图（观察单变量数据分布）、分位数-分位数图（观察分布到分布的关系）、直方图（观察数据的分布）、散点图（观察两个变量的具体分布）

数据的相似性度量

• 列联表（Contingency Table）：描述两个属性之间的关系。对二元属性： $q$ 为均为 $1$ 的记录数， $r,s$ 分别为 $A,B$ 属性为 $1$ 的记录数， $t$ 为 $A,B$ 属性均为 $0$ 的记录数。

• 相异度：对称的二元属性，相异度 $d$ 为 $d = \frac{r + s}{q + r + s + t}$；非对称的二元属性，相异度 $d = \frac{r + s}{q + r + s} = 1 - \frac{q}{q + r + s} = 1 - \text{ Jacard}(A,B)$ （对于非对称的相似度, 负匹配数目 $t$ 被忽略）。

• 距离度量

  • 曼哈顿距离（Manhattan Distance）：$d_{\text{manhattan }}(A,B) = \sum(|A_{i} - B_{i}|)$

  • 欧氏距离（Euclidean Distance）：$d_{\text{euclidean }}(A,B) = \sqrt{\sum(\left( A_{i} - B_{i} \right)^{2})}$

• 其他相似性度量：余弦相似性（向量内积空间的夹角）、马氏距离（考虑数据局部分布的距离度量）、相关系数（皮尔森系数，衡量两个变量的线性关系）、KL散度（数据分布比较）。

数据标准化：

• 最小-最大标准化：$x^{\prime}_{i} = \frac{x_{i} - \min}{\max - \min}$

• Z-score 标准化：$z_{i} = \frac{x_{i} - \text{ mean}}{s}$

  • 其中 $s$ 为平均绝对偏差（MAD）或标准差，前者为 $s = \frac{1}{n}\sum|x_{i} - \text{ mean}|$，比标准差更具有鲁棒性。

数据预处理

大纲要求：

• 了解：数据压缩，主成分分析等方法。

• 理解：数据预处理的原因和重要性，数据清理的任务。

• 掌握：数据规约的基本策略，数据集成的方法，数据变化的方法。

数据质量的维度

• 准确性（Accuracy）：数据正确反映现实世界的程度。

• 完整性（Completeness）：数据中缺失信息的程度。

• 一致性（Consistency）：数据在不同源或时间点的一致性。

• 时效性（Timeliness）：数据的及时更新。

• 可信性（Believability）：数据是否被用户信赖。

• 可解释性（Interpretability）：数据是否容易理解。

数据预处理的任务

• 数据清理：处理空缺值、噪声数据、删除孤立点、解决不一致性。

  • 空缺值处理：忽略元组、人工填写、使用全局变量填充、用平均值填充（属性样本的平均值、同一类所有样本的平均值）、用最可能的值填充（使用像 Bayesian 公式或判定树这样预测的方法）。

  • 噪声数据处理：分箱（binning）、聚类、回归。

    • 分箱：将数据排序后分成若干个区间，然后可以按箱的平均值平滑、按箱中值平滑、按箱的边界平滑等等。

    • 聚类：使用聚类算法将数据分成若干个类，监测并去除离群点。

• 数据集成：集成多个数据库、数据立方体或文件。

  • 冗余数据处理：数值型数据的相关分析、标称数据的卡方检验（如，使用卡方检验来检测两个分类变量的独立性）。

• 数据归约：得到数据集的压缩表示，但可以得到相同或相近的结果。

  • 维归约：小波分析、PCA、特征筛选（如，使用PCA来减少数据的维度）。

  • 数量归约：直方图、回归、聚类、抽样、数据立方体聚集（如，使用直方图来归约连续数据）。

  • 数据压缩：有损压缩和无损压缩（如，使用有损压缩来减少音频文件的大小）。

• 数据变换：规范化和聚集。

  • 规范化：最小-最大规范化、Z-score 规范化、小数定标规范化。

• 离散化和概念分层：将连续数据划分为区间，或将标称数据替换为高层概念（如，将年龄数据离散化为“青年”、“中年“、“老年“）。

关联规则挖掘

大纲要求：

• 了解： Apriori 关联规则挖掘各种改进方法和约束关联规则挖掘。

• 理解： FP 增长树挖掘关联规则的方法和思想。

• 掌握： Apriori 算法及其过程，基本概念如频繁项集，支持度，置信度等。

关联规则

• 支持度$\text{Support}(X) = \frac{|t \in T~|~X \subseteq t|}{|T|}$：包含 X 的事务的比例。

• 置信度$\text{Confidence}(X \rightarrow Y) = \frac{\text{Support}(X \cup Y)}{\text{Support}(X)} = \frac{|t \in T~|~X \cup Y \subseteq t|}{|t \in T~|~X \subseteq t|}$：Y 在包含 X 的事务中出现的频繁程度。

• 频繁项集（Frequent Itemset）：支持度$\geq$ min_sup 的项集。

• 关联规则（Association Rule）：支持度$\geq$ min_sup 并且置信度$\geq$ min_conf 的规则。

Apriori 算法

Apriori 性质：

1. 如果一个项集是频繁的，那么它的所有子集也是频繁的。

2. 如果一个项集是非频繁的，那么它的所有超集也是非频繁的。

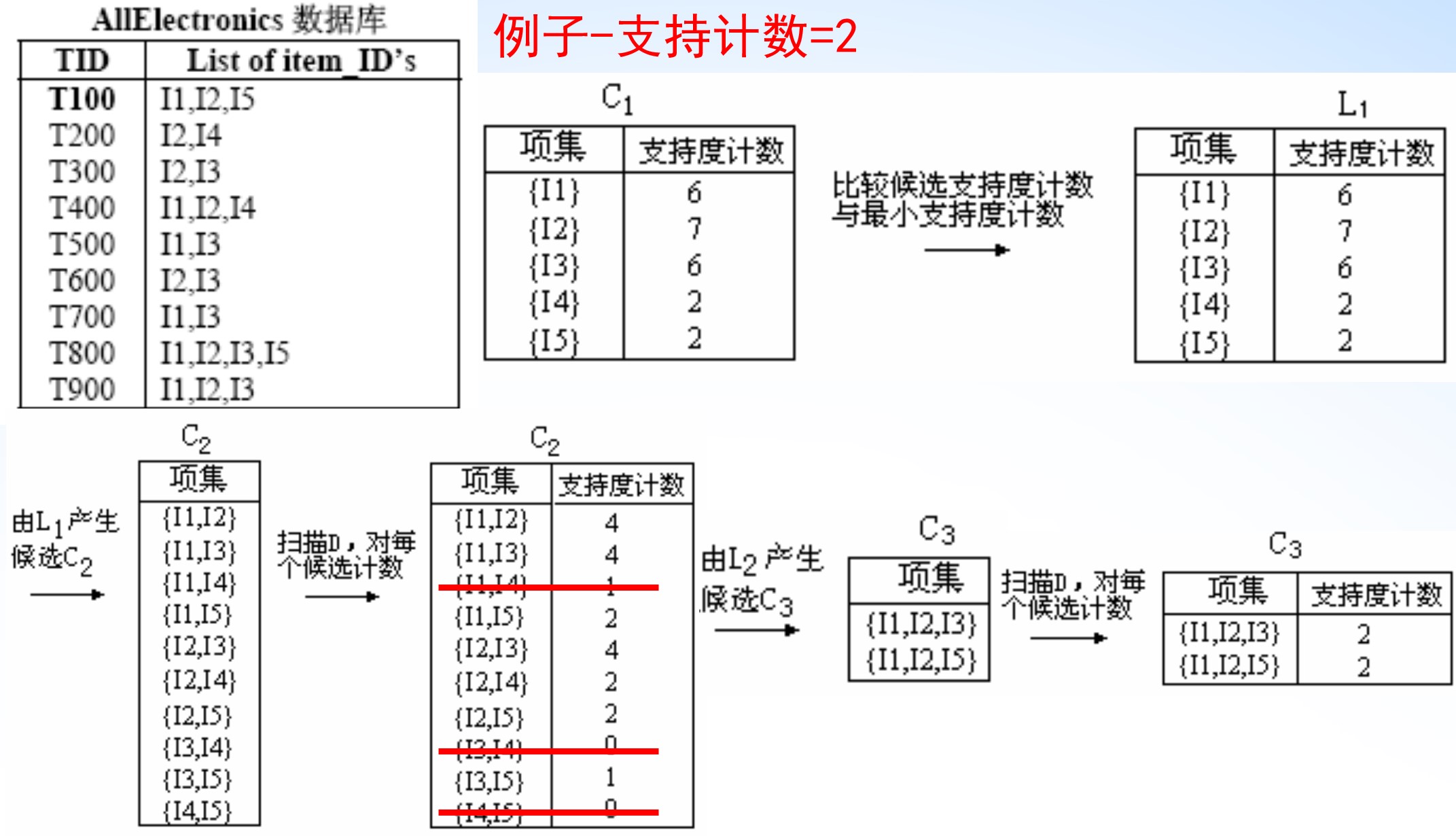
Apriori 算法步骤：

1. 生成频繁项集

2. 生成频繁 1 项集

3. 生成频繁 $k + 1$ 项集

   1. 自连接：连接 $k$ 项集生成 $k + 1$ 项集 （频繁的项的所有子集均为频繁的）

   2. 剪枝：删除非频繁的 $k + 1$ 项集

4. 重复直到没有频繁项集产生

5. 生成关联规则：将每个频繁项集划分为两个非空子集，计算置信度

Apriori 算法的挑战：

• 事务数据库的多次扫描

• 大量的候选集生成

• 候选支持度计数的繁重计算量

Apriori 算法的改进：

• 散列项集计数：使用哈希表来计数项集的支持度，若一个桶的计数小于 min_sup ，则该桶对应的项集不可能是频繁的。

• 事务压缩：不包含任何频繁 $k$ 项集的事务不可能包含任何频繁 $k + 1$ 项集。因此这些事务在其后的考虑中，可以加上标记或删除。

• 基于分区的方法：将数据集分为多个分区，每个分区独立处理，然后合并结果。

• 采样：对数据集进行采样，然后在采样数据上运行 Apriori 算法，最后将结果推广到整个数据集。

FP-Growth 算法

FP-Growth算法步骤

1. 构建 FP-Tree

   1. 扫描数据集，统计每个项的频率，按照支持度递减排序，删除非频繁项

   2. 再次扫描数据集，对于每个事务，按照频繁项的频率递减排序，从根节点开始依次插入节点 / 增加 1 的计数

2. 根据 FP-Tree 生成频繁项集 （似乎不考察）

   1. 从 FP-Tree 的底部开始，对于每个项，找到条件模式基，递归构建条件 FP-Tree

   2. 对于每个条件 FP-Tree，递归生成频繁项集

节点链在手算的时候不要也无所谓，是用在计算机算法中找到下一个相同元素的位置，用于构建条件 FP-Tree。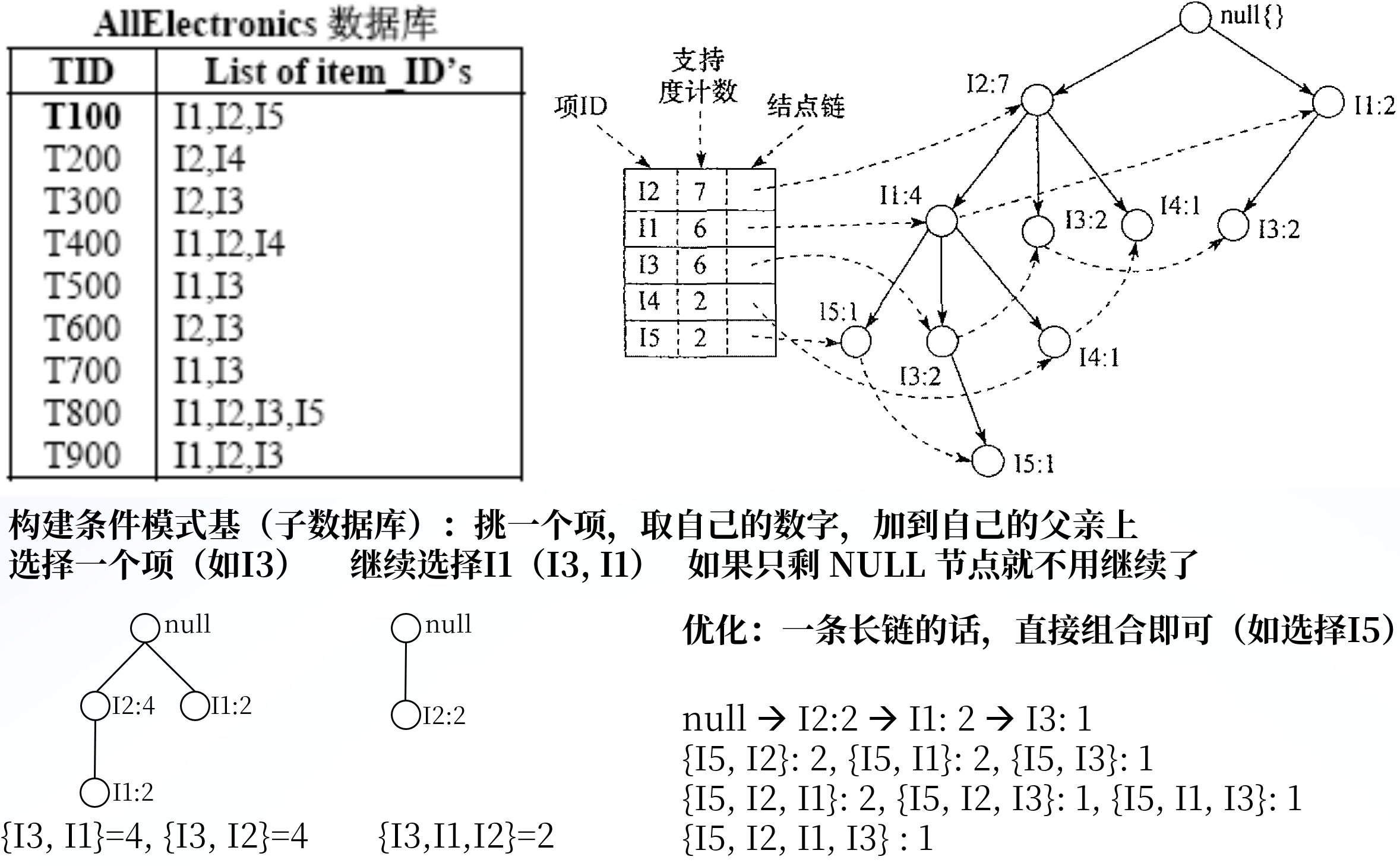

关联规则的评价

高置信度的规则并不一定有足够的价值，甚至有时会误导用户（如，高置信度的规则可能是由于低支持度的项集导致的）。

• 提升度（Lift）：规则的置信度与项集的支持度的比值。 $\text{Lift}(X \rightarrow Y) = \frac{\text{Confidence}(X \rightarrow Y)}{\text{Support}(Y)}$

• 兴趣因子（Interest Factor）：二元属性的提升度。 $\text{Interest Factor}(X,Y) = \frac{\text{Support}(X \cup Y)}{\text{Support}(X) \times \text{ Support}(Y)}$

分类

大纲要求：

• 了解：评估分类算法准确性的几个基本指标。

• 理解： SVM 分类算法的基本思想想。

• 掌握： ID3 和 C4.5 分类算法、 KNN 算法和朴素贝叶斯分类算法方法。

分类的风险

• 经验风险：分类器在样本数据上的分类的结果与真实结果（因为样本是已经标注过的数据，是准确的数据）之间的差值。

• 置信度：分类器在新数据上的分类结果与真实结果之间的差值。

• 结构风险：经验风险和置信度的综合。

结构风险最小化原则是机器学习的一个重要原则。结构风险最小化原则认为，学习算法应该在经验风险和置信度之间寻找一个平衡，以期望在新数据上有更好的分类效果。

影响风险的几个因素：

• 样本容量：样本容量越大，学习结果越可能接近真实结果，置信风险越小。

• 分类函数的 VC 维：VC 维越大，推广能力越差，置信风险越大。（ VC 维：是对函数类的一种度量，可以简单的理解为问题的复杂程度， VC 维越高，一个问题就越复杂，越难解决）

分类器评价准则

混淆矩阵（ Confusion Matrix ）： T/F 表示真/假（分类对错）， P/N 表示正/负（分类结果）。正样本数为 $P = \text{ TP } + \text{ FN}$，分类为正样本数为 $P^{\prime} = \text{ TP } + \text{ FP}$。

• 准确率（Accuracy）：分类正确的样本数占总样本数的比例。 $\text{Accuracy } = \frac{\text{TP } + \text{ TN}}{P + N}$

• 精确率（Precision）：分类为正类的样本实际为正类的比例。 $\text{Precision } = \frac{\text{ TP}}{P^{\prime}}$

• 召回率（Recall）：实际为正类的样本被分类为正类的比例。 $\text{Recall } = \frac{\text{ TP}}{P}$

• F1 值：精确率和召回率的调和平均。 $F1\ = \frac{2\left( \text{Precision } \times \text{ Recall} \right)}{\text{Precision } + \text{ Recall}}$

类不平衡时考虑的指标：

• 灵敏度（Sensitivity）：实际为正类的样本被分类为正类的比例。也就是召回率。 $\text{Sensitivity } = \text{ Recall } = \frac{\text{ TP}}{P}$

• 特异度（Specificity）：实际为负类的样本被分类为负类的比例。 $\text{Specificity } = \frac{\text{ TN}}{N}$

决策树

1. 树以代表训练样本的单个结点开始

2. 如果样本都在同一个类．则该结点成为树叶，并用该类标记

3. 否则，根据某个属性将样本分为不同的子集，每个子集对应一个分支

4. 对每个子集递归地应用相同的过程

5. 停止条件：所有样本属于同一类、没有属性可用于分裂、达到树的最大深度

优点：

• 简单、易于理解

• 有一定可解释性，可以提取规则

缺点：

• 容易过拟合，泛化能力差

• 对噪声敏感，尤其是分支较多时

决策树的属性选择度量

• 又称分裂规则，决定给定节点上的元组如何分裂

• 具有最好度量得分的属性（对分出的数据类别越“纯”）选定为分裂属性

选择度量：（ $p_{i}$ 为类别 $i$ 的概率， $D_{j}$ 为划分后的子集）

• 信息熵（Entropy）：数据的混乱程度，越小越好。 $\text{Info}(D) = - \sum_{i = 1}^{m}p_{i}\log_{2}p_{i}$

• 信息增益（Information Gain）：划分前后信息熵的差值。 $\text{Gain}(D,A) = \text{ Info}(D) - \text{ Info}(D,A)$，其中 $\text{Info}(D,A) = \sum_{j = 1}^{v}\frac{|D_{j}|}{|D|}\text{ Info}\left( D_{j} \right)$，其中 $D$ 被 $A$ 划分为 $v$ 个子集 $D_{j}$。

• 增益率（Gain Ratio）：信息增益与划分信息的比值。 $\text{GainRatio}(D,A) = \frac{\text{ Gain}(D,A)}{\text{SplitInfo}(D,A)}$，其中 $\text{SplitInfo}(D,A) = - \sum_{j = 1}^{v}\frac{|D_{j}|}{|D|}\log_{2}\frac{|D_{j}|}{|D|}$ ，可以看为划分的信息熵。

• Gini 指数：划分前后基尼指数的差值，度量数据元组的不纯度，越小越好。 $\text{Gini}(D) = 1 - \sum_{i = 1}^{m}p_{i}^{2}$，其中 $p_{i}$ 为类别 $i$ 的概率；数据集 $D$ 被 $A$ 划分为两个子集 $D_{1}$ 和 $D_{2}$，则 $\text{Gini}(D,A) = \frac{|D_{1}|}{|D|}\text{ Gini}\left( D_{1} \right) + \frac{|D_{2}|}{|D|}\text{ Gini}\left( D_{2} \right)$；如果是三个属性，要进行二元分裂，那么两两为一组，计算基尼指数，选择最小的基尼指数。

信息增益（ ID3 ）倾向于有大量不同取值的属性，但是每个划分只有一个类的时候 info=0。C4.5 (ID3 后继) 使用增益率来克服这一问题(规范化信息增益)。 CART 使用 Gini 指数。

决策树的过拟合

一棵归纳的树可能过分拟合训练数据：

• 分枝太多,某些反映训练数据中的异常，噪音/孤立点

• 对未参与训练的样本的低精度预测

解决方法：

• 剪枝（ Pruning ）：预剪枝（在树的构建过程中进行剪枝）和后剪枝（在树构建完成后进行剪枝）。

  • 预剪枝：在树的构建过程中，当某个节点的分裂不能带来足够的信息增益 / 度量时，停止分裂。

  • 后剪枝：在树构建完成后，对树进行剪枝，将一些子树替换为叶子节点。

• 集成学习（ Ensemble Learning ）：将多个分类器集成在一起，通过投票或加权投票来决定最终的分类结果。

K-近邻算法（ K-Nearest Neighbor ）

有那么一堆你已经知道分类的数据，然后当一个新数据进入的时候，就开始跟训练数据里的每个点求距离，然后挑出离这个数据最近的K个点，看看这K个点属于什么类型，然后用少数服从多数的原则，给新数据归类。

算法步骤：

1. 算距离：给定测试对象，计算它与训练集中的每个对象的距离；

2. 找邻居：圈定距离最近的k个训练对象，作为测试对象的近邻；

3. 做分类：根据这k个近邻归属的主要类别，来对测试对象分类。

优点：

1. 简单，易于理解，易于实现，无需估计参数，无需训练

2. 准确率一般较高

3. 适合对稀有事件进行分类，特别适合于多分类问题

缺点：

1. 懒惰算法，对测试样本分类时的计算量大，内存开销大，评分慢

2. 不平衡时，倾向于将类全部归类为大类

3. 可解释性较差，无法给出决策树那样的规则

4. 对噪声非常敏感

朴素贝叶斯分类

朴素贝叶斯是一种基于贝叶斯定理和特征条件独立假设的分类方法。贝叶斯分类算法是统计学的一种分类方法，它是一类利用概率统计知识进行分类的算法。

类条件独立假设：假设每个属性在给定类别下是独立的： $$P\left( y~|~x_{1},x_{2},\ldots,x_{n} \right) = P(y)P\left( x_{1}~|~y \right)P\left( x_{2}~|~y \right)\ldots P\left( x_{n}~|~y \right)$$

贝叶斯分类器的决策规则： $$\hat{y} = \arg\max\limits_{y}P(y)\prod_{i = 1}^{n}P\left( x_{i}|y \right)$$

优点：

1. 简单，易于实现，速度快，可以应用于大规模数据集

2. 准确率较高，可以与决策树和神经网络分类算法相媲美

缺点：

1. 朴素贝叶斯分类器的独立性假设在实际应用中往往不成立，因此分类性能不一定很高

2. 朴素贝叶斯分类器的先验概率的准确性对分类结果影响较大

支持向量机（ Support Vector Machine ）

支持向量机是一种二类分类模型，它的基本模型是定义在特征空间上的间隔最大的线性分类器，间隔最大使得支持向量机有别于其他分类器的独特性。

支持向量机的基本思想是通过间隔最大化，找到一个最优的超平面，将不同类别的样本分开。

支持向量机的优点：

1. 间隔最大化，泛化能力强

2. 可以解决高维问题

3. 在小样本数据上表现良好

支持向量机的缺点：

1. 需要线性可分，或者可以通过核函数映射到高维空间后线性可分

人工神经网络（ Artificial Neural Network ）

人工神经网络是一种模仿生物神经网络的结构和功能的数学模型，用于对函数进行估计或近似。神经网络由大量的人工神经元组成，每个神经元与其他神经元相连，每个连接对应一个权值，神经元的输出是通过非线性激活函数处理加权和得到的。

• 优点

  • 预测精度总的来说较高

  • 健壮性好，训练样本中包含错误时也可正常工作

  • 输出可能是离散值、连续值或者是离散或量化属性的向量值

  • 对目标进行分类较快

• 缺点

  • 训练（学习）时间长

  • 蕴涵在学习的权中的符号含义很难理解

  • 很难根专业领域知识相整合

多层前馈神经网络

• 输入层：是网络与外部环境打交道的地方，它接收外部输入模式，并由输入单元传送给相连隐层各单元；

• 隐层：是网络的内部处理单元层，神经网络具有模式变换能力，如模式分类、模式完善、特征抽取等，主要体现在隐层单元的处理。根据模式变换功能的不同，隐层可以有多层，也可以没有。由于隐层单元不直接与外部输入输出打交道，故通常将中间层称为隐层；

• 输出层：是网络产生输出模式并与显示设备或执行机构打交道的地方。

集成学习

集成学习是一种机器学习范式，通过构建并结合多个学习器来完成学习任务。集成学习的基本原理是：一群弱学习器的集合，可以组合成一个强学习器。集成学习的目标是通过结合多个学习器的学习结果，获得比单个学习器更好的泛化性能。

实际中，要获得好的集成，个体学习器通常应该“好而不同”，即个体学习器要有一定的“准确性”，并且要有“多样性”，即学习器间具有差异。

• 同质的：基学习器是同质的，即同质集成中的基学习器是同种类型的学习器，如同是决策树、同是神经网络等。

• 异质的：基学习器是异质的，即异质集成中的基学习器是不同类型的学习器，如决策树、神经网络、支持向量机等。

集成学习的方法：

• Bagging：通过自助采样法，从原始训练集中有放回地重复抽样产生多个不同的训练集，然后分别训练多个基学习器，再将这些基学习器集成（使用投票法或平均法）。

• 随机森林( Random Forset, RF )：是 Bagging 的一个扩展。RF 在 以决策树为基学习器 构建 Bagging 集成的基础上，在决策树的训练过程中引入随机属性选择。传统决策树在选择划分属性时是在当前节点的所有属性集合中选择一个最优属性；而在 RF 中，对基决策树的每个结点，先从该结点的属性集合中随机选择一个包含 k 个属性的子集，然后再从这个子集中选择一个最优属性用于划分。参数 k 控制了随机性的引入程度。

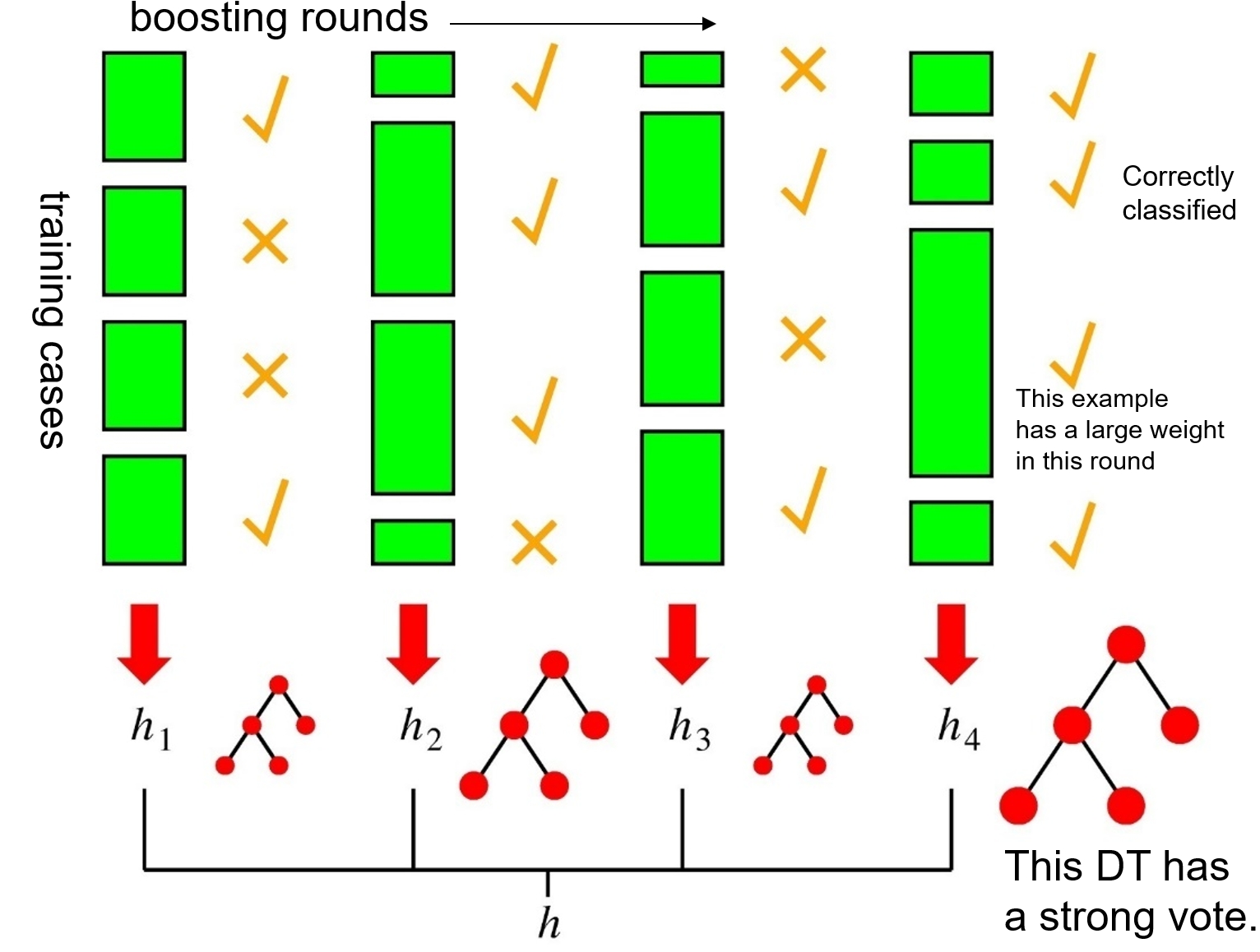
• Boosting：是一种串行式集成学习方法，可将弱学习器提升为强学习器的算法：先从初始训练集训练出一个基学习器，再根据基学习器的表现对训练样本进行调整，使得先前基学习器做错的训练样本在后续受到更多的关注，然后基于调整后的样本训练下一个基学习器，如此重复进行，直至基学习器达到事先指定的值，最终将这 T 个基学习器进行加权结合（权重通常是基学习器的准确率）。

• Stacking：是一种集成学习方法，通过将多个基学习器的学习结果作为新的训练集，来训练一个次级学习器。在这个新数据集中，初级学习器的输出被当作样例输入特征，而初始样本的标记仍被当作样例标记。

聚类

大纲要求：

• 了解：聚类的广泛应用，基于聚类的噪声点检测。

• 理解：聚类分析基本概念，聚类分析中的数据类型。

• 掌握：聚类分析中的各种数据类型的处理方法；最简单的划分方法和层次方法(AGNES)。

聚类是无监督学习的一种，就是将数据分为多个簇(Clusters)，使得在同一个簇内对象之间具有较高的相似度，而不同簇之间的对象差别较大，目的是寻找数据中潜在的自然分组结构 ，让一个簇内的数据尽可能相似，不同簇的数据尽可能不同。

一般而言，从不同的角度出发可以将各种聚类算法分成不同的类型。如按照聚类的基本思想可主要分为：

1. 基于划分方法（partitioning method）
   给定一个有n个对象的数据集，划分聚类技术将构造数据k个划分，每一个划分就代表一个簇。对于给定的k，算法首先给出一个初始的划分方法，以后通过反复迭代的方法改变划分，使得每一次改进之后的划分方案都较前一次更好。
   经典的算法有：K-Means（K-均值）, K-Medoids（K-中心点）等

2. 基于层次的方法（hierarchical method）
   层次聚类方法对给定的数据集进行层次的分解，直到某种条件满足为止
   凝聚的层次聚类：一种自底向上的策略，首先将每个对象作为一个簇，然后合并这些原子簇为越来越大的簇，直到某个终结条件被满足。AGNES算法
   分裂的层次聚类：采用自顶向下的策略，它首先将所有对象置于一个簇中，然后逐渐细分为越来越小的簇，直到达到了某个终结条件。DIANA算法

3. 基于密度的方法（density-based method）
   密度聚类方法的指导思想是，只要一个区域中的点的密度大于某个阈值，就把它加到与之相近的聚类中去。这类算法能克服基于距离的算法只能发现“类圆形”的聚类的缺点，可发现任意形状的聚类，且对噪声数据不敏感

4. 基于网格的方法（grid-based method）
   将对象空间量化为有限数目的单元，形成一个网格结构，所有的聚类都在这个网格结构中上进行。

K-Means 算法

K-Means 算法是一种基于划分的聚类算法，它将数据集划分为 K 个簇，每个簇的中心是簇中所有点的均值，使得簇内对象互相相似，簇间差异大。

聚类目标函数：簇对象到簇中心平方误差准则最小化。

$$E = \sum_{i = 1}^{K}\sum_{x \in C_{i}}\| x - u_{i}\|^{2},u_{i} = \frac{1}{|C_{i}|}\sum_{x \in C_{i}}x$$

K-Means 算法步骤：

1. 选择 K 个初始中心

2. 对每个样本，计算其到 K 个中心的距离，将其划分到距离最近的簇

3. 更新每个簇的中心

4. 重复 2、3 步，直到中心不再变化

优点：

• 算法简单，容易实现

• 计算量不大，收敛速度快

• 对处理大数据集，该算法保持可伸缩性和高效性

缺点：

• 需要事先确定 K 的值

• 对初始值敏感

• 对噪声和离群点敏感

• 不适合发现非球形簇或大小差别很大的簇

AGNES 算法

AGNES (Agglomerative Nesting) 是一种基于层次的聚类算法，它是一种自底向上的聚类方法，首先将每个对象作为一个簇，然后合并这些原子簇为越来越大的簇，直到某个终结条件被满足。

AGNES 算法步骤：

1. 将每个对象作为一个簇

2. 计算两两簇之间的距离（根据两个簇中最近的数据点之间的距离）

3. 合并距离最近的两个簇

4. 重复 2、3 步，直到满足终止条件

优点：

• 不需要事先确定簇的个数

• 可以发现任意形状的簇

• 可以发现嵌套的簇

缺点：

• 计算复杂度高

• 对噪声和离群点敏感

DBSCAN 算法

DBSCAN （ Density-Based Spatial Clustering of Applications with Noise ）是一种基于密度的聚类算法，它将具有足够高密度的区域划分为簇，并可以利用类的高密度连通性，在噪声点的空间数据库中发现任意形状的簇。

其中心思想是：对于一个类中的每个对象，在其给定半径的领域中包含的对象不能少于某一给定的最小数目。在 DBSCAN 中，发现一个类的过程是基于这样的事实：一个类能够被其中的任意一个核心对象所确定。

基本概念：

• 核心对象：在半径 $\varepsilon$ 内至少包含 MinPts 个对象

• 直接密度可达：如果 $p$ 在 $q$ 的 $\varepsilon$ 邻域内，并且 $q$ 是核心对象，则 $p$ 直接密度可达于 $q$

• 密度可达：存在一条 $p_{1},p_{2},\ldots,p_{n}$ 的路径，其中 $p_{1} = p$，$p_{n} = q$，并且 $p_{\left\{ i + 1 \right\}}$ 直接密度可达于 $p_{i}$，则 $p$ 密度可达于 $q$

• 密度相连：存在一个核心对象 $o$，使得 $p$ 和 $q$ 都密度可达于 $o$，则 $p$ 和 $q$ 密度相连

• 噪声点：不是核心对象，也不密度可达于任何核心对象的点

DBSCAN 算法步骤：

1. 选择一个未被访问的对象 $p$，找到其 $\varepsilon$ 邻域内的所有对象

2. 如果 $p$ 的邻域内的对象数目大于 MinPts （为核心对象），则创建一个新簇，将 $p$ 加入簇中，然后对 $p$ 的邻域内的每个对象进行同样的操作（找出所有密度可达的对象）

3. 如果 $p$ 的邻域内的对象数目小于 MinPts ，将 $p$ 标记为噪声点

优点：

• 可以发现任意形状的簇

• 不需要事先确定簇的个数

• 可以发现噪声点

缺点：

• 对参数 $\varepsilon$ 和 MinPts 敏感，但是参数需要靠经验调整

• 如果数据库比较大的时候要进行大量的I/O 开销。

离群点

离群点是一个数据对象，它显著不同于其它数据对象，好像它是被不同的机制产生的一样。

异常数据具有特殊的意义和很高的实用价值 ，异常数据虽然有时候会作为离群点被排斥掉，但是却也有可能给我们新的视角，比如在诈骗和入侵过程中。

离群点类型：

• 全局离群点：和别的点一点关系都没有

• 局部离群点：对全局来说不是离群点，但是对某个簇来说是离群点

• 集体离群点：某一个集体和其他不同

局部异常因子（ Local Outlier Factor, LOF ）

局部异常因子（LOF）是一种基于密度的离群点检测算法，它通过比较每个数据点的局部密度与其邻居的局部密度来检测离群点。

有关概念：

• $k$-距离：一个点 $p$ 到某个点 $o$ 的距离 $\text{dist}_{k}(p) = d(p,o)$，使得：

  • 至少存在 $k$ 个点 $o^{\prime}$ 满足 $d(p,o^{\prime}) \leq d(p,o)$

  • 至多存在 $k - 1$ 个点 $o^{\prime\prime}$ 满足 $d(p,o^{\prime\prime}) < d(p,o)$

• $k$-邻域：所有到 $p$ 的距离不大于 $k$-距离的点的集合

• 可达距离：点 $p$ 到点 $o$ 的可达距离 $\text{reachdist}_{k}(p,o) = \max(\text{dist}_{k}(o),d(p,o))$ （注意区分公式中的 $p$ 和 $o$）

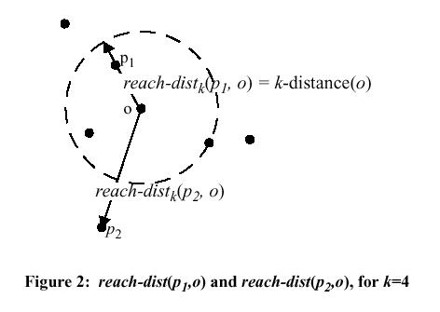
对象 $p$ 的局部可达密度(Local Reachable Distance) ${lrd}_{k}(p)$ 是对象 $p$ 的 $k$-邻域中对象的平均可达距离的倒数：

$${lrd}_{k}(p) = 1/\left( \frac{\sum_{o \in N_{k}(p)}\text{ reachdist}_{k}(p,o)}{|N_{k}(p)|} \right)$$

局部异常因子（LOF）是对象 $p$ 的局部可达密度与其邻居的局部可达密度之比的平均值：

$$LOF_{k}(p) = \frac{\sum_{o \in N_{k}(p)}\frac{{lrd}_{k}(o)}{{lrd}_{k}(p)}}{|N_{k}(p)|}$$

LRD 是局部密度，所以孤立点的密度小，分子大，分母小，所以最终结果大。对象 $p$ 的局部异常因子表示 $p$ 的异常程度，局部异常因子愈大，就认为它更可能异常；反之则可能性小。

哈希

大纲要求：

• 了解：大数据产生的背景和原因。

• 理解： Hadoop、Spark 的思想及架构。

• 掌握：大数据特点、哈希技术、数据流挖掘和大数据处理平台。

本文将这一章划分为：哈希、数据流、大数据处理平台三个部分。

大数据挖掘面临的一些问题：

• 高维诅咒问题

• 存储问题

• 检索速度问题

三个关键技术：

• Shingling: 变换文档、邮件等转换成集合。

• Minhashing: 变换规模大的集合到规模小的“签名”，并且保留原有的相似性，使得集合表示的特征矩阵转成签名矩阵。

• Locality-sensitive hashing: 集中找出签名矩阵中相似的签名对。

Shingling

Shingling 是一种将文档、邮件等转换成集合的方法。Shingling 的基本思想是将文档转换成 k-gram 集合，然后将 k-gram 集合转换成集合表示。

如 abcab 的 2-gram 集合为 {ab, bc, ca, ab}。

一个文档可以通过 k-gram 的集合来很好表示，两个文档相似性通过它们的 k-gram 的集合的相似度表示。

MinHashing

MinHashing 将集合表示成特征矩阵，其中每一列 C 到签名矩阵的对应列 Sig(C) 满足:

• Sig(C) 表示 C 后，其对应长度要足够小.

• 两个集合的相似度Sim (C1, C2) 等价于两个签名Sig (C1) 与 Sig (C2) 的相似度.

MinHashing 算法步骤：

1. 计算特征矩阵：取集合的全集，每个元素对应一列，每个集合对应一行，若集合包含该元素，则对应位置为 1，否则为 0。

2. 生成随机排列：随机生成 $k$ 个排列 $\{ h_{1i}\},\{ h_{2i}\},\ldots,\{ h_{ki}\}$。

3. 计算签名矩阵：对于每个排列，计算每个集合的最小哈希值，将其作为签名矩阵的一列。

可以证明有 $\text{Sim}\left( C_{1},C_{2} \right) = \Pr(h\left( C_{1} \right) = h\left( C_{2} \right))$ ，但实际可能不会完全相等。

Locality-sensitive hashing

Locality-sensitive hashing (LSH) 是一种将相似的对象映射到同一个桶中的技术，它可以用于快速检索相似对象。

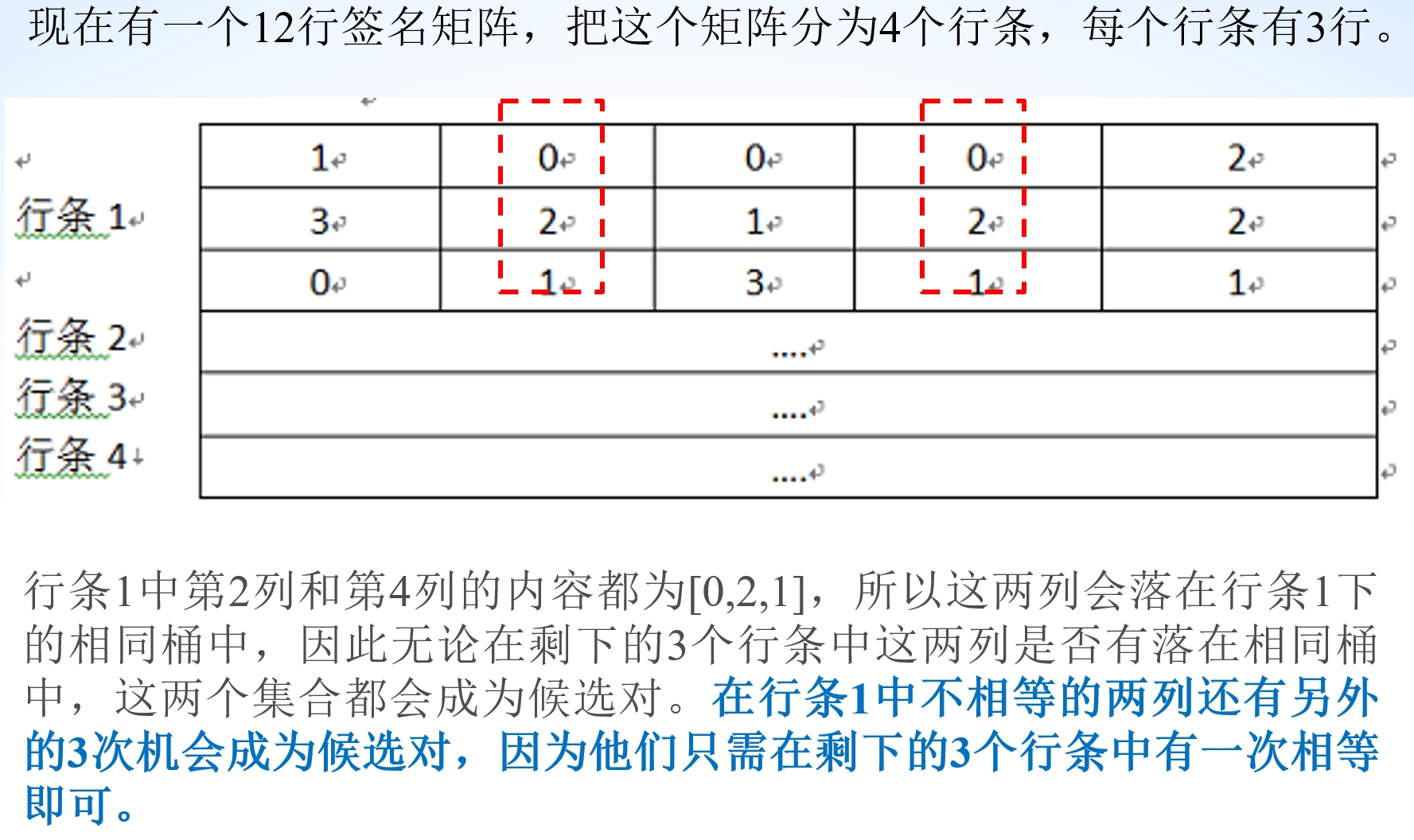
1. 将 Signature Matrix 分成一些 bands ，每个 bands 包含一些 rows 。

2. 然后把每个 band 哈希到一些 bucket 中，注意 bucket 的数量要足够多（筛选：设定 bucket 个数，然后比对，相同的颜色部分扔到相应的篮子里面）。

3. 计算相似性。使得两个不一样的 bands 被哈希到不同的 bucket 中，如果两个 document 的bands中至少有一个 share 了同一个 bucket ，那这两个 document 就是 candidate pair ，也就是很有可能是相似的。

哈希函数可以考虑使用超平面，如 $h(x) = \text{ sign}\left( r^{\top}x \right)$。

数据流挖掘

数据流挖掘是一种处理数据流的技术，数据流是一个巨大的数据对象序列，具有一些独特的特征：、逐个、可能无界、概念漂移

挑战：单程处理、内存限制、低时间复杂度、概念漂移

数据流挖掘的目标是从数据流中提取有价值的信息，如频繁项集、聚类、分类、异常检测等。

概念漂移

概念漂移是指数据流中的概念随时间的推移而发生变化。概念漂移是数据流挖掘中的一个重要问题，因为数据流中的概念可能随时间的推移而发生变化，导致模型的性能下降。

概念漂移的类型：

• $P(C)$ 漂移：数据分布发生变化

• $P(X)$ 漂移：输入的分布发生变化，但是输出属性不变

• $P\left( C|X \right)$ 漂移：虽然输入的分布没有变化，但是输出属性发生了变化，是真正的概念漂移

概念漂移的检测方法：

• 基于统计的方法：对不同时间窗口（大小固定或不固定）的数据，统计 $P\left( C|X \right)$ 的变化
  问题：窗口大小不好确定、学习漂移慢、会出现假漂移
  ADWIM 算法：自适应窗口大小的概念漂移检测算法，根据数据的分布自适应调整窗口大小，发现了显著性变化后，就用新的代替老的

• 错误率检测方法：监控分类器的错误率，当错误率超过阈值时，认为发生了概念漂移
  问题：对噪声敏感、无法检测小的或缓慢的漂移、对学习器的健壮性要求高

数据流分类

每次输入一个数据，分类器就要对这个数据快速做出分类，然后继续处理下一个数据。

快速决策树

快速决策树是一种用于数据流分类的决策树算法，它通过对数据流进行随机采样，然后构建决策树，以减少计算量。

快速决策树算法步骤：

1. 从数据流中随机采样一部分数据，构建决策树

2. 对新数据进行分类时，沿着决策树进行分类

3. 当数据流中新数据满足 $\Delta\overline{G} = \overline{G}(X_{a}) - \overline{G}(X_{b}) > \varepsilon$ 时，重新构建决策树

如果错误率超过阈值，重新构建决策树。

数据流聚类

数据流聚类是一种处理数据流的技术，它通过对数据流进行聚类，发现数据流中的潜在模式。分为在线和离线两个阶段：线上把数据用合适的数据结构处理，线下用传统方式去进行聚类。

微簇

微簇是数据流聚类中的一个重要概念，它是一组彼此接近的数据点，将被视为一个单元，用于进一步的离线宏聚类。

微簇的簇特征 $\text{CF } = (N,LS,SS)$，其中 $N$ 是簇中的数据点数，$LS$ 是簇中数据点的线性和，$SS$ 是簇中数据点的平方和。做这些统计量的目的是为了能够计算簇的中心和半径，且可以动态地更新。

大数据平台

大数据平台的功能：

• 容纳海量数据：利用计算机群集的存储和计算能力。不仅在性能上有所扩展，而且其处理传入的大量数据流的能力也相应提高。

• 速度快：列式数据库架构(相对于基于行的非并行处理传统数据库)和使用大规模并行处理技术，不仅能够大幅提高性能(通常约100到1000倍)，还可以实现更低且更透明的定价机制。

• 兼容传统工具：确保平台已经过认证，可以兼容传统工具。

• 利用 Hadoop ： Hadoop 已成为大数据领域中的主要平台。利用 Hadoop 作为用于持久性和轻量型数据管理的高效益平台。

• 为数据科学家提供支持：数据科学家在企业 IT 中拥有着更高的影响力和重要性，快速、高效、易于使用和广泛部署的大数据平台可以帮助拉近商业人士和技术专家之间的距离。

• 提供数据分析功能：确保大数据平台不仅支持在数秒钟内准备并加载数据，还支持利用高级算法建立预测模型，轻松部署模型以进行数据库内计分。同时使数据科学家能够使用现有统计软件包和首选语言。

Hadoop

Hadoop 是一个软件框架，用于跨大型计算机集群对大型数据集进行分布式处理 TB PB 级别。

Hadoop 核心设计： HDFS 和 MapReduce 。Hadoop 以一种可靠、高效、可伸缩的方式进行数据处理。

Hadoop 的优点：

• 高可靠性：按位存储和处理数据的能力值得信赖，能可靠存储和处理 PB 级别的数据。

• 高扩展性：在可用的计算机集群间分配数据并完成计算任务，这些集群可以方便地扩展到数以千计的节点中。

• 高效性：能以并行的工作方式够在节点之间动态地移动数据，并保证各个节点的动态平衡，因此处理速度非常快。

• 高容错性：能够自动保存数据的多个副本，并且能够自动将失败的任务重新分配。

• 低成本：开源的，项目的软件成本因此会大大降低，并可以使用普通计算机组成集群。

Hadoop 的组件：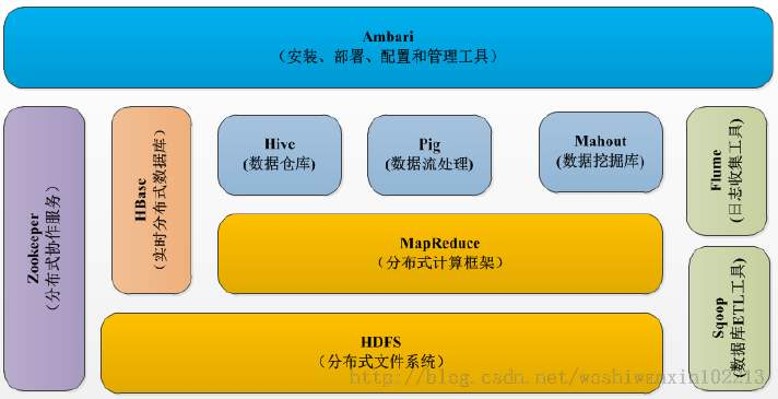

主要是 HDFS 和 MapReduce 两个核心组件：

• HDFS ： Hadoop 分布式文件系统。分为 NameNode 和 DataNode 两种节点， NameNode 负责管理文件系统的命名空间， DataNode 负责存储文件块。需要数据的时候， NameNode 会告诉客户端去哪里找数据块，然后客户端直接和 DataNode 通信。 Datanode 存储实际数据，文件被存在各个节点里，拥有时钟机制，每隔几秒发送一次汇报工作，如果过了很久还没发送，那么默认你已经挂掉，重新创建节点存储被挂掉节点存储的数据

• MapReduce ： Hadoop 分布式计算框架。 Mapreduce 适用于一次操作，对多次操作不适用，共享机制落后，花费大量时间 IO

Spark

Spark 是一个基于内存计算的大数据并行计算框架，它提供了高效的数据抽象，可以在内存中快速计算，比 Hadoop MapReduce 更快。

RDD 弹性分布式数据集：是 Spark 的核心概念，是一个不可变的分布式对象集合，可以在集群上并行操作。

RDD 的操作方式：

• Transformation ：对 RDD 进行转换操作，生成新的 RDD

• Action ：对 RDD 进行行动操作，触发计算并返回结果