数值分析复习整理

本复习资料不以讲解为目的，建议勿以此为学习资料。

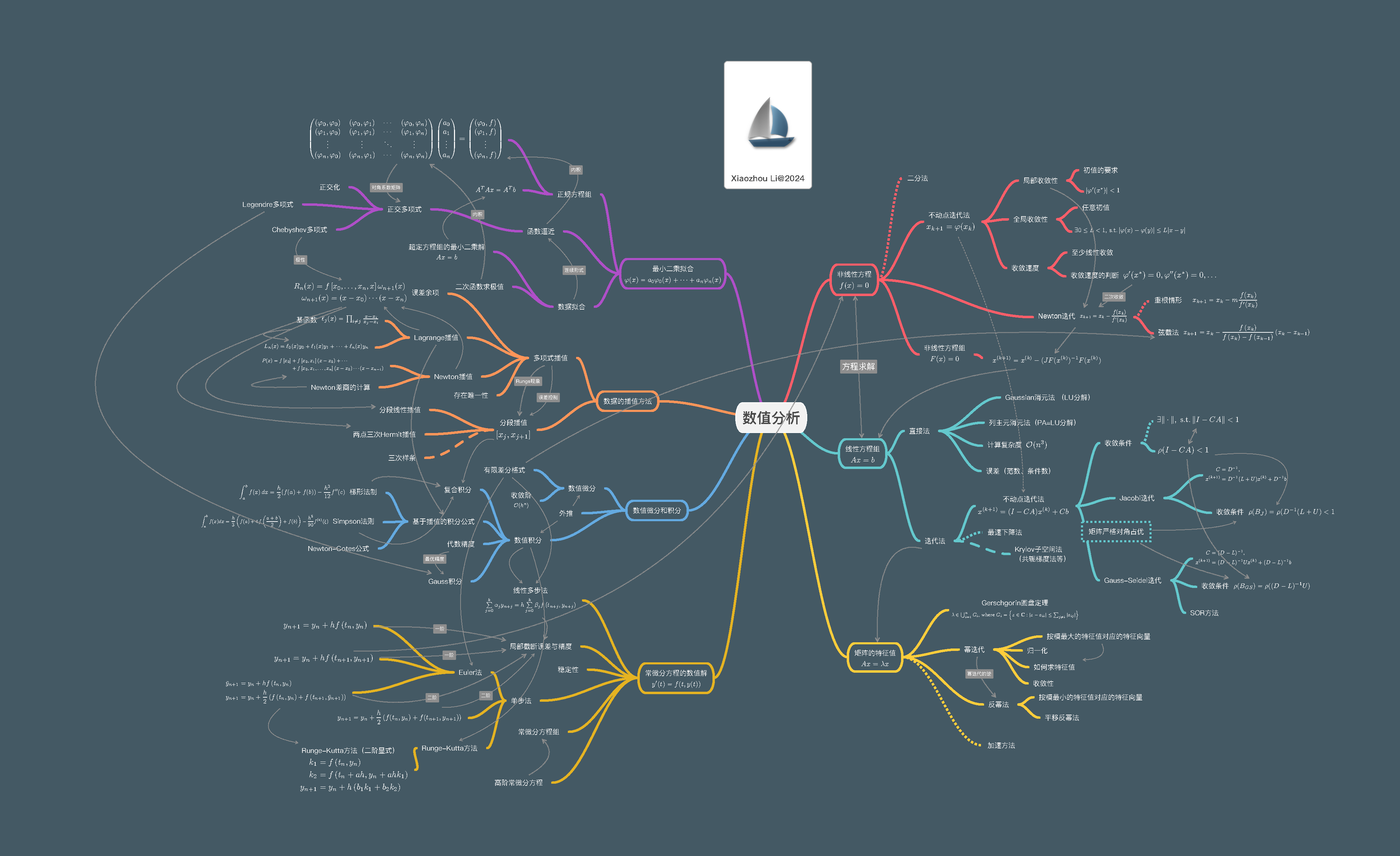
李小舟老师的总结思维导图，做得太好了，放在这里作为开头。 这里可以下载PDF版本

基本概念

几个性质

• 适定性（well-posedness）：解的存在唯一性
  适定性是对问题的描述

• 稳定性（stability）：解的连续性
  稳定性是对算法的描述

• 收敛性（convergence）：解的逼近性

线性方程组

$$Ax = b$$

基本概念

• 向量范数：非负、齐次、正定、三角不等式
  对$p$范数的定义：$\| x\|_{p} = \left( \sum_{i = 1}^{n}|x_{i}|^{p} \right)^{\frac{1}{p}}$
  所有范数等价（等价的定义）
  $(x,y) \leq \| x\|_{2}\| y\|_{2}$

• 矩阵范数：几乎所有都使用向量范数定义
  $\| A\|_{p} = \max\frac{\| Ax\|_{p}}{\| x\|_{p}} = \max\limits_{\| x\|_{p} = 1}\| Ax\|_{p}$
  常用的矩阵范数：

  • $1$-范数：列和最大值，$\| A\|_{1} = \max\limits_{1 \leq j \leq n}\sum_{i = 1}^{m}|a_{ij}|$

  • $2$-范数：$A^{T}A$的谱半径，$\| A\|_{2} = \sqrt{\lambda_{\max}\left( A^{T}A \right)}$

  • $\infty$-范数：行和最大值，$\| A\|_{\infty} = \max\limits_{1 \leq i \leq m}\sum_{j = 1}^{n}|a_{ij}|$

  • $F$-范数：特例，并非由向量范数导出，$\| A\|_{F} = \sqrt{\sum\sum|a_{ij}|^{2}}$

• 谱半径：$\rho(A) = \max|\lambda_{i}|$
  谱半径不超过任何矩阵范数（证明：$\|\lambda u\| = \| Au\| \leq \| A\|\| u\|$）

方程组的性态

• 余量：$r = b - Ax$
  一般认为，$\| r\|$越小，解的精度越高。（但也有例外）

• 条件数：$\text{cond}(A) = \| A\|\| A^{- 1}\|$ （A非奇异）

  • $\text{cond}(A) \geq 1$（$\| AA^{- 1}\| \leq \| A\|\| A^{- 1}\|$）

  • $\text{cond}(A)$越大，方程组的解越不稳定，即这个问题越病态（ill-conditioned）。

  • $\forall\alpha \neq 0,\text{cond}(\alpha A) = \text{cond}(A)$

求解病态方程组，一般用$PAx = Pb$使得$\text{cond}(PA)$尽可能小。

高斯消元法

• 顺序高斯消元法（等价于 LU 分解）：

  1. 对增广矩阵进行消元操作，得到上三角矩阵；

  2. 从下往上回代，得到解。

• 列主元高斯消元法（等价于 PA = LU 分解）：
  每次选取当前列中绝对值最大的元素所在的行，与当前行交换，其他的与顺序高斯消元法相同。

LU分解（直接三角分解）

存在性：$A$非奇异，且$A$的所有主子式都非零，$A$的LU分解 存在且唯一 。

1. $A = LU$，其中$L$为下三角矩阵，$U$为上三角矩阵，且$\text{diag}(L)$或$\text{diag}(R)$全为$1$。

2. 问题变为$LUx = b$，即求解$Ly = b$和$Ux = y$。

TODO: PA=LU、追赶法、平方根法

迭代法

相容性：$x^{\ast} = Bx^{\ast} + f$

• Jacobi迭代法：$A = D - L - U$，字面含义，直接剖开即可。
  $Dx_{k + 1} = (L + U)x_{k} + b \Longrightarrow x_{k + 1} = D^{- 1}(L + U)x_{k} + D^{- 1}b$。

• Gauss-Seidel迭代法：对Jacobi迭代法的改进
  $Dx_{k + 1} = Lx_{k + 1} + Ux_{k} + b \Longrightarrow x_{k + 1} = (D - L)^{- 1}Ux_{k} + (D - L)^{- 1}b$。

• 逐次超松弛迭代法（SOR）：Gauss-Seidel迭代后加上松弛因子$\omega$
  $x_{k + 1} = (1 - \omega)x_{k} + \omega{\widetilde{x}}_{k + 1}$。
  $\forall A \in R^{n \times n}$且$a_{ii} \neq 0$有$\forall\omega$，$\rho(B_{\omega}) \geq |\omega - 1|$
  类似的也有 JOR。
  SOR 部分相关内容可参考 CSDN的一篇博客。

对角占优矩阵

• 严格对角占优：$|a_{ii}| > \sum_{j \neq i}|a_{ij}|$对所有$i$成立。

• 对角占优：$|a_{ii}| \geq \sum_{j \neq i}|a_{ij}|$对所有$i$成立且至少有一个严格大于。

迭代收敛定理

收敛的一般证明方法：取$e_{k} = x_{k} - x^{\ast}$，证明所给的条件下$\| e_{n}\| \rightarrow 0$。

$x_{k + 1} = Bx_{k} + f$ 收敛$\Longleftrightarrow \rho(B) < 1$。（充分条件：任意一个范数小于$1$即可）

当$A$严格对角占优时，Jacobi迭代法、Gauss-Seidel迭代法、SOR迭代法（$0 < \omega \leq 1$）都收敛。

SOR 收敛$\Longrightarrow |\omega - 1| < 1$；$A$ 对称正定且 $|\omega - 1| < 1 \Longrightarrow$ SOR 收敛。

收敛率与收敛速度

要使得$\| e_{k}\| \leq \sigma\| e_{0}\|$，可以让$\| B^{k}\| \leq \sigma$，变换后可得到$k \geq \frac{- \ln\sigma}{- \ln\| B^{k}\|^{\frac{1}{k}}}$。

平均收敛率：$R_{k}(B) = - \ln\| B^{k}\|^{\frac{1}{k}}$

渐进收敛速度（收敛速度）：$R(B) = - \ln\rho(B)$

使用$R(B)$近似替代$R_{k}(B)$可近似得到$k$的取值。

TODO: 共轭梯度

非线性方程

基本概念

• 单根与重根：$f(x) = \left( x - x^{\ast} \right)^{m}g(x),m \in N_{+}$，则$x = x^{\ast}$是$f(x) = 0$的$m$重根。

二分法

若$f(x) \in C\lbrack a,b\rbrack$且$f(a)f(b) < 0$，则$f(x) = 0$在$\lbrack a,b\rbrack$上有至少一个根，$\lbrack a,b\rbrack$为有根区间。

二分法即不断取中点，取新的有根区间，直至满足精度要求。

优点：好算，可靠，有大范围的收敛性。

缺点：收敛速度慢，不适用于区间内有多个根的情况。

不动点迭代法

$f(x) = 0 \Rightarrow x = \varphi(x) \Rightarrow x_{k + 1} = \varphi(x_{k})$，若$\left\{ x_{k} \right\}$有极限，则极限为$f(x) = 0$的根。

若$\varphi(x)$连续，可得到$x^{\ast} = \varphi(x^{\ast})$。$x^{\ast}$ 被称为不动点。

收敛性：$\forall x \in \lbrack a,b\rbrack,\varphi(x) \in \lbrack a,b\rbrack$且$|\varphi^{\prime}(x)| \leq L < 1$，则问题在$\lbrack a,b\rbrack$上有唯一的根且迭代法收敛。

局部收敛性：$\varphi(x)$在$x = x^{\ast}$的某个邻域连续，且$|\varphi^{\prime}\left( x^{\ast} \right)| < 1$，则迭代法局部收敛。

迭代收敛的阶

$$\lim\limits_{k \rightarrow \infty}\frac{|x_{k + 1} - x^{\ast}|}{|x_{k} - x^{\ast}|^{p}} = c \neq 0$$

$p$为迭代收敛的阶。

• $p = 1,0 < c < 1$：线性收敛

• $1 < p < 2$ 或 $p = 1,c = 0$：超线性收敛

• $p = 2$：二次收敛

若\varphi^{^{\prime}}(x^{\ast}) = \varphi^{^{\prime}}^{\prime}\left( x^{\ast} \right) = \ldots = \varphi^{\left( (p - 1) \right)\left( x^{\ast} \right)} = 0 且 $\varphi^{\left( (p) \right)\left( x^{\ast} \right)} \neq 0$，则迭代法的收敛阶为$p$，且：$$\lim\limits_{k \rightarrow \infty}\frac{|x_{k + 1} - x^{\ast}|}{|x_{k} - x^{\ast}|^{p}} = \frac{\varphi^{(p)}\left( x^{\ast} \right)}{p!}$$

特别地，$|x^{\ast} - x_{k + 1}| = |\varphi(x^{\ast}) - \varphi(x_{k})| = |\varphi^{^{\prime}}(\xi)||x^{\ast} - x_{k}|$。若$|\varphi^{^{\prime}}(x^{\ast})| \neq 0$，则迭代法收敛。

牛顿法

$f(x) \approx f\left( x_{k} \right) + f^{^{\prime}}(x_{k})\left( x - x_{k} \right) = 0$，取$$x_{k + 1} = x_{k} - \frac{f\left( x_{k} \right)}{f^{^{\prime}}(x_{k})}$$

收敛性：若$f\left( x^{\ast} \right) = 0,f^{^{\prime}}\left( x^{\ast} \right) \neq 0$且二次连续可微，则牛顿法局部收敛，且收敛阶为$2$。

牛顿法的重根情况

若$f(x){= \left( x - x^{\ast} \right)}^{m}g(x)$，则$\varphi^{^{\prime}}(x) = 1 - \frac{1}{m}$。当$m > 1$时，$0 < \varphi^{^{\prime}}(x^{\ast}) < 1$，线性收敛。

令$\mu = \frac{f\left( x^{\ast} \right)}{f^{^{\prime}}(x^{\ast})}$，则$x^{\ast}$为$\mu(x)$的单根，牛顿法修改为$\varphi(x) = x - \frac{\mu(x)}{\mu^{^{\prime}}(x)}$（求重根的迭代公式）

割线法

用差商代替牛顿法中的导数，即$$x_{k + 1} = x_{k} - f\left( x_{k} \right)\left( \frac{f\left( x_{k} \right) - f\left( x_{k - 1} \right)}{x_{k} - x_{k - 1}} \right)^{- 1}$$

收敛性：超线性收敛。

插值

拟合函数在节点处的函数值与插值函数在节点处的函数值相等（$f\left( x_{i} \right) = p\left( x_{i} \right)$）。

插值条件：$\left( x_{i},f\left( x_{i} \right) \right)$

Lagrange插值

$$l_{i}(x) = \prod_{j \neq i}\frac{x - x_{j}}{x_{i} - x_{j}},p(x) = \sum_{i = 0}^{n}f\left( x_{i} \right)l_{i}(x)$$

Lagrange 插值余项：$E(x) = f(x) - p(x) = \frac{f^{(n + 1)}(\xi)}{(n + 1)!}P_{(n + 1)(x)},\xi \in \lbrack a,b\rbrack$

其中$P_{(n + 1)(x)} = \prod_{i = 0}^{n}\left( x - x_{i} \right)$

Lagrange 插值余项$E(x)$的推导：

由定义得$E\left( x_{i} \right) = 0,i = 0,1,\ldots,n$，因此令$E(x) = Q(x)P_{(n + 1)(x)}$，其中$Q(x)$为待定函数。作函数$\varphi(x) = f(x) - L_{n}(x) - Q\left( x^{\ast} \right)P_{(n + 1)(x)}$，其中$x^{\ast}$为异于$x_{0},x_{1},\ldots,x_{n}$的点，因此$\varphi(x)$有$n + 2$个零点，由 Rolle 定理可得$\varphi^{(n + 1)}$有$n + 1$个零点，递推得到$\varphi^{(n + 1)}$存在一个零点$t = \xi$，因此$$\varphi^{(n + 1)}(\xi) = f^{(n + 1)}(\xi) - 0 - Q\left( x^{\ast} \right)(n + 1)! = 0 \Rightarrow Q\left( x^{\ast} \right) = \frac{f^{(n + 1)}(\xi)}{(n + 1)!}$$

缺点：加入节点需要重新计算所有的插值多项式。

Newton插值

差商

$k$阶差商：

$$f\left\lbrack x_{0},x_{1},\ldots,x_{k} \right\rbrack = \frac{f\left\lbrack x_{1},x_{2},\ldots,x_{k} \right\rbrack - f\left\lbrack x_{0},x_{1},\ldots,x_{k - 1} \right\rbrack}{x_{k} - x_{0}}$$

差商具有对称性（交换节点不影响差商的值）。

差商表

利用$f\left\lbrack x_{0},x_{1},\ldots,x_{k - 1} \right\rbrack$与$f\left\lbrack x_{1},x_{2},\ldots,x_{k} \right\rbrack$计算$f\left\lbrack x_{0},x_{1},\ldots,x_{k} \right\rbrack$。

Newton插值多项式

$$\begin{aligned} f(x) & = f\left\lbrack x_{0} \right\rbrack & & + f\left\lbrack x_{0},x_{1} \right\rbrack\left( x - x_{0} \right) + f\left\lbrack x_{0},x_{1},x_{2} \right\rbrack\left( x - x_{0} \right)\left( x - x_{1} \right) + \ldots \\ & & & + f\left\lbrack x_{0},x_{1},\ldots,x_{n} \right\rbrack\left( x - x_{0} \right)\left( x - x_{1} \right)\ldots\left( x - x_{n - 1} \right) \\ & & & + f\left\lbrack x,x_{0},x_{1},\ldots,x_{n} \right\rbrack\left( x - x_{0} \right)\left( x - x_{1} \right)\ldots\left( x - x_{n} \right) \\ & = N_{n}(x) & & + f\left\lbrack x,x_{0},x_{1},\ldots,x_{n} \right\rbrack P_{n + 1}(x) \end{aligned}$$

插值余项：$E(x) = f(x) - N_{n}(x) = f\left\lbrack x,x_{0},x_{1},\ldots,x_{n} \right\rbrack P_{n + 1}(x)$

$\Rightarrow f\left\lbrack x,x_{0},x_{1},\ldots,x_{n} \right\rbrack = \frac{f^{n + 1}(\xi)}{(n + 1)!}$

Hermite插值

不仅给出函数值，还给出导数值。给出$n + 1$个节点，$r + 1$个导数值，共$n + r + 2$个条件。

构造基函数的步骤：

1. 明确基函数的次数

2. 如果$\alpha(x_{k}) = \alpha^{^{\prime}}\left( x_{k} \right) = \ldots = \alpha^{r - 1}\left( x_{k} \right) = 0$，则说明$x_{k}$是一个$r$重根，$\alpha(x_{k}) = \left( l_{k}(x) \right)^{r}g(x)$

3. $g(x)$由基函数的次数与已经确定的条件决定，设置为通用的多项式（如$ax + b$）

4. 将其他条件代入，解出$g(x)$的系数

分段插值

将插值区间分为若干段，每段使用一个插值多项式。

• 线性插值：$p(x) = f\left( x_{i} \right) + \frac{f\left( x_{i + 1} \right) - f\left( x_{i} \right)}{x_{i + 1} - x_{i}}\left( x - x_{i} \right)$

• 三次 Hermite 插值：有每个点的函数值和导数值，每个区间使用一个三次多项式。

Runge 现象

TODO

拟合

函数的内积、范数与正交性

设$f(x),g(x)$在$\lbrack a,b\rbrack$上连续，定义内积为：

$$(f,g) = \int_{a}^{b}f(x)g(x)dx$$

定义范数：

• $\| f\|_{1} = \int_{a}^{b}|f(x)|dx$

• $\| f\|_{2} = \sqrt{(f,f)}$

• $\| f\|_{\infty} = \max\limits_{a \leq x \leq b}|f(x)|$

若函数系列$\left\{ \varphi_{i} \right\}$满足$\left( \varphi_{i},\varphi_{j} \right) = 0,i \neq j$，则称其为正交函数系。

Gram 矩阵与正则方程

设$\Phi = \left\{ \varphi_{1},\varphi_{2},\ldots,\varphi_{n} \right\}$，则$\Phi$的 Gram 矩阵 $G$ 满足 $G_{i,j} = \left( \varphi_{i},\varphi_{j} \right)$。

函数系线性无关的充要条件是 $\det G \neq 0$。

正则方程为 $Ga = b$，其中 $a = \left( a_{1},a_{2},\ldots,a_{n} \right)^{T}$，$b = \left( \left( f,\varphi_{1} \right),\left( f,\varphi_{2} \right),\ldots,\left( f,\varphi_{n} \right) \right)^{T}$。

正则方程也可以写为 $A^{T}Aa = A^{T}f$，其中 $A = \left( \varphi_{1},\varphi_{2},\ldots,\varphi_{n} \right)$。

函数逼近

设$X$为线性赋范空间，$\Phi$为$X$的子空间。给定$f \in X$，若存在$\varphi \in \Phi$，使得$\| f - \varphi\|$最小，则称$\varphi$为$f$在$\Phi$上的最佳逼近。当取二范数时，$\varphi$为$f$在$\Phi$上的最佳平方逼近；取无穷范数时，$\varphi$为$f$在$\Phi$上的最佳一致逼近。

最佳二次逼近

唯一性：$f(x)$ 在给定的 $\Phi$ 上的最佳二次逼近 $\varphi(x)$ 是唯一的。

设最佳逼近为 $\varphi(x) = a_{0}\varphi_{0}(x) + \cdots + a_{m}\varphi_{m}(x)$，则余项 $$\| E(x)\|_{2}^{2} = \left( f - y^{\ast},f - y^{\ast} \right) = \| f\|_{2}^{2} - \sum_{j = 0}^{m}a_{j}^{\ast}\left( f,\varphi_{j} \right)$$

若记正则方程为 $Ga = b$，则余项为 $\| E(x)\|_{2}^{2} = \| f\|_{2}^{2} - b^{T}a$

多项式作二次逼近

只需讨论$\lbrack 0,1\rbrack$上的多项式逼近。取 $\Phi = \left\{ 1,x,x^{2},\ldots,x^{n} \right\}$，则 $G$ 为 $n + 1$ 阶的 Hilbert 矩阵（$H_{ij} = \frac{1}{i + j - 1}$）。计算$\left( (f,1),(f,x),\ldots,\left( f,x^{n} \right) \right)^{T}$，解出$a$即可。

Hilbert 矩阵是一个病态矩阵，其条件数随着阶数的增加而迅速增大。

正交多项式作二次逼近

若取正交多项式作为基函数，则 $G$ 为对角矩阵。因此：$$a_{j} = \frac{\left( f,\varphi_{j} \right)}{\left( \varphi_{j},\varphi_{j} \right)},y^{\ast (x)} = \sum_{j = 0}^{n}a_{j}\varphi_{j}(x)$$

Legendre 多项式

$$P_{n}(x) = \frac{1}{2^{n}n!}\frac{d^{n}}{dx^{n}}\left( x^{2} - 1 \right)^{n}$$

Legendre 的正交区间为 $\lbrack - 1,1\rbrack$。

$$a_{j}^{\ast} = \frac{2j + 1}{2}\int_{- 1}^{1}f(x)P_{j}(x)dx,E(x) = \| f\|_{2}^{2} - \sum_{j = 0}^{n}\frac{2}{2j + 1}\left( a_{j}^{\ast} \right)^{2}$$

一个递推公式：$(n + 1)P_{n + 1} = (2n + 1)xP_{n} - nP_{n - 1}$

Chebyshev 多项式

$$T_{n}(x) = \cos(n\arccos x)$$

TODO

最小二乘数据拟合

设数据为 $\left\{ \left( x_{i},f_{i} \right) \right\}$，$y(x) = \text{ argmin}_{\varphi \in \Phi}\sum_{i = 1}^{n}\left( f_{i} - \varphi(x_{i}) \right)^{2}$为最小二乘拟合。

最小二乘存在且唯一。

多项式最小二乘拟合

设 $\Phi = \left\{ 1,x,x^{2},\ldots,x^{n} \right\}$，则 $G$ 为 $n + 1$ 阶的 Vandermonde 矩阵$$G_{i,j} = \sum_{k = 0}^{n}x_{k}^{i + j},b_{j} = \sum_{i = 1}^{n}f_{i}x_{i}^{j}$$

可以列表计算：$i,x_{i},x_{i}^{2},\ldots,x_{i}^{n},f_{i},f_{i}x_{i},\ldots,f_{i}x_{i}^{n}$

如果函数合适，可以做变换使得问题变为线性拟合问题。

数值积分

$\int_{a}^{b}f(x)dx = \sum_{j = 0}^{n}A_{j}f\left( x_{j} \right) + E(f)$，$A_{j}$为与$x_{j}$相关而与$f$无关的求积系数，$E(f)$为余项。

代数精度

若求积公式对所有次数不超过$n$的多项式成立而至少有一个次数为$n + 1$的多项式不成立，则称该求积公式具有$n$次代数精度。

定理：给定$n + 1$个互异的节点$x_{0},x_{1},\ldots,x_{n}$，则总存在相应的求积系数$A_{0},A_{1},\ldots,A_{n}$，使得求积公式至少具有$n$次代数精度。

插值型求积公式

由 Lagrange 插值多项式 $f(x) = \sum_{i = 0}^{n}f\left( x_{i} \right)l_{i}(x) + \frac{f^{n + 1}(\xi)}{(n + 1)!}P_{n + 1}(x)$，两边同时积分，得到插值型求积公式：$A_{j} = \int_{a}^{b}l_{j}(x)dx$。

Newton-Cotes 求积公式

将区间$\lbrack a,b\rbrack$等分为$n$个区间，步长为$h\frac{= (b - a)}{n}$，则求积节点为$x_{i} = a + ih$

令$x = a + th$，则$$l_{j}(x) = \prod_{k \neq j}\frac{x - x_{k}}{x_{j} - x_{k}} = \prod_{k \neq j}\frac{t - k}{j - k}$$

代入得到$$A_{j} = \int_{a}^{b}l_{j}(x)dx = \frac{( - 1)^{n - j}h}{j!(n - j)!}\int_{0}^{n}\prod_{k \neq j}(t - k)dt$$

令$C_{j} = \frac{A_{j}}{b - a} = \frac{( - 1)^{n - j}}{n \cdot j!(n - j)!}\int_{0}^{n}\prod_{k \neq j}(t - k)dt$，则求积公式为$$\int_{a}^{b}f(x)dx = (b - a)\sum_{j = 0}^{n}C_{j}f\left( x_{j} \right) + E$$

取$f(x) \equiv 1$，得到$\sum C_{j} = 1$。

• 梯形公式：$n = 1,C_{0} = C_{1} = \frac{1}{2},E = - \frac{h^{3}}{12}f^{^{\prime\prime}}(\xi)$

• Simpson 公式：$n = 2,C_{0} = C_{2} = \frac{1}{6},C_{1} = \frac{4}{6},E = - \frac{h^{5}}{90}f^{(4)}(\xi)$

• $\ldots$

当$n$为偶数时，$n + 1$个节点的 Newton-Cotes 求积公式至少具有$n + 1$次代数精度。

稳定性：TODO

复化求积公式

将区间$\lbrack a,b\rbrack$等分为$n$个小区间，每个小区间使用次数较低的求积公式，得到复化求积公式。$n$常取为$2^{k}$。

复化梯形公式

令$T_{n}$为$n$个梯形公式的和，容易得到$T_{n} = \frac{h}{2}\left( f(a) + 2\sum_{i = 1}^{n - 1}f\left( x_{i} \right) + f(b) \right)$。进一步将每个小区间二等分，记$U_{n} = h\sum_{i = 0}^{n - 1}f\left( x_{i + \frac{1}{2}} \right)$为二等分点的和乘以$n$等分的步长，则$T_{2n} = \frac{1}{2}\left( T_{n} + U_{n} \right)$。

余项：TODO

复化 Simpson 公式

$S_{n} = \frac{h}{6}\sum(f\left( x_{i} \right) + 4f\left( x_{i + \frac{1}{2}} \right) + f\left( x_{i + 1} \right)) = \frac{1}{3}T_{n} + \frac{2}{3}U_{n} = \frac{4T_{2n} - T_{n}}{4 - 1}$

余项：TODO

变步长

给定$\varepsilon$，直到$|S_{2^{k}} - S_{2^{k - 1}}| < \varepsilon$，停止计算。

Romberg 求积

由泰勒展开可以得到$$I = \int_{a}^{b}f(x)dx = \frac{h}{2}\left( f(a) + 2\sum_{i = 1}^{n - 1}f\left( x_{i} \right) + f(b) \right) + \sum_{j = 1}^{\infty}\alpha_{j}h^{2j} \triangleq T(h) - \sum_{j = 1}^{\infty}\alpha_{j}h^{2j}$$其中$T(h)$为复化梯形公式的值。利用 Romberg 外推的技巧对这个值进行外推： $$\begin{cases} T_{0}(h) \triangleq T(h) = I + \alpha_{1}h^{2} + \alpha_{2}h^{4} + \ldots \\ T\left( \frac{h}{2} \right) = I + \alpha_{1}\frac{h^{2}}{4} + \alpha_{2}\frac{h^{4}}{16} + \ldots \end{cases} \Rightarrow T_{1}(h) \triangleq \frac{4T\left( \frac{h}{2} \right) - T(h)}{4 - 1} = I + \beta_{1}h^{4} + \ldots$$ 我们记$T_{m}(h)$误差的阶为$h^{2(m + 1)}$。$T_{1}(h)$为复化 Simpson 公式，$T_{2}(h)$为复化 Cotes 公式，但再往后的公式与 Newton-Cotes 就没有直接联系了。

为了方便计算，将区间$\lbrack a,b\rbrack$等分为$2^{k}$份，记复化梯形公式为$T_{0,k}$。由前面的推导可得： $$\begin{aligned} T_{0,0} & = \frac{b - a}{2}\left( f(a) + f(b) \right),U_{0,0} = (b - a)f\left( \frac{a + b}{2} \right) \\ U_{0,k - 1} & = \frac{b - a}{2^{k - 1}}\sum_{i = 1}^{2^{k - 1}}f\left( a + (2i - 1)\frac{b - a}{2^{k}} \right),T_{0,k} = \frac{1}{2}\left( T_{0,k - 1} + U_{0,k - 1} \right) \\ T_{m,k} & = \frac{4^{m}T_{m - 1,k + 1} - T_{m - 1,k}}{4^{m} - 1} \end{aligned}$$

可以列表计算：

$$	$m = 0$	$m = 1$	$m = 2$	$m = 3$
$i = 0$	$T_{0,0}$	$$	$$	$$
$i = 1$	$T_{0,1}$	$T_{1,0}$	$$	$$
$i = 2$	$T_{0,2}$	$T_{1,1}$	$T_{2,0}$	$$
$i = 3$	$T_{0,3}$	$T_{1,2}$	$T_{2,1}$	$T_{3,0}$

Gauss 求积

Newton-Cotes 求积公式的节点是等距的，而 Gauss 求积公式通过选取合适的节点，使得求积公式具有更高的代数精度。对于有$n + 1$个节点的 Gauss 求积公式，其代数精度至少为$2n + 1$，可以通过此定义利用待定系数法求解（取$f(x) = 1,x,\ldots,x^{2n + 1}$，方程组具有$2n + 2$个方程，$2n + 2$个未知数（$A_{0}\sim A_{n},x_{0}\sim x_{n}$），解出待定系数即可）。

原理：对 Hermite 插值多项式左右两边同时积分，则有$$\int_{a}^{b}f(x)dx = \sum_{i = 0}^{n}H_{i}f\left( x_{i} \right) + \sum_{i = 0}^{n}{\overline{H}}_{i}(x)f^{^{\prime}}\left( x_{i} \right) + \frac{f^{(2n + 2)}(\xi)}{(2n + 2)!}\int_{a}^{b}P_{n + 1}^{2}(x)dx$$ ，其中$H$与$\overline{H}$由$h$与$\overline{h}$积分得到。现选取合适的节点使得${\overline{H}}_{i}(x) = 0$，则有$\int_{a}^{b}f(x)dx = \sum_{i = 0}^{n}H_{i}f\left( x_{i} \right) + E(f)$。

定理：$x_{0},\ldots,x_{n}$为 Gauss 点$\Leftrightarrow \omega(x) = \prod_{k = 0}^{n}\left( x - x_{k} \right)$与任意次数不超过$n$的多项式正交。

通过这条定理，取一个正交多项式系$\left\{ \varphi_{0},\varphi_{1},\ldots,\varphi_{n},\varphi_{n + 1} \right\}$，则取$\varphi_{n + 1}$的根作为 Gauss 点即可。

Gauss-Legendre 求积

取区间$\lbrack - 1,1\rbrack$，$\varphi_{n}$为 Legendre 多项式（$P_{n}(x) = \frac{1}{2^{n}n!}\frac{d^{n}}{dx^{n}}\left( x^{2} - 1 \right)^{n}$），$x_{i}$为 Legendre 多项式的根，$A_{i} = \frac{2}{\left( 1 - x_{i}^{2} \right)\left( \varphi_{n + 1}^{^{\prime}}\left( x_{i} \right) \right)^{2}}$，Gauss 点为$\varphi_{n + 1}$的零点。

其他的 Gauss 求积

Chebyshev 多项式：权函数为$\frac{1}{\sqrt{1 - x^{2}}}$，区间为$\lbrack - 1,1\rbrack$，Chebyshev 多项式$T_{n + 1}(x)$的根为$x_{j} = \cos(\frac{2j + 1}{2n + 2}\pi)$，求积系数为$A_{j} = \frac{\pi}{n + 1}$。

Laguerre 多项式：权函数为$e^{- x}$，区间为$\lbrack 0, + \infty)$，TODO。

Hermite 多项式：权函数为$e^{- x^{2}}$，区间为$( - \infty, + \infty)$，TODO。

对于有权函数的 Gauss 求积，所求积分的形式为$\int_{a}^{b}\rho(x)f(x)dx$，其中$\rho(x)$为权函数。解为$\sum_{j = 0}^{n}A_{j}f\left( x_{j} \right)$而不是$\sum_{j = 0}^{n}A_{j}\rho(x_{j})f\left( x_{j} \right)$

数值微分

Lagrange 插值多项式求数值微分

对 Lagrange 插值多项式求导即可得到数值微分的结果。 $$f^{(k)}(x) = \sum_{i = 0}^{n}f\left( x_{i} \right)l_{i}^{(k)}(x) + \left( E(x) \right)^{(k)}$$

差商代替微商求函数的数值微分

向前差商：f^{^{\prime}}(x) = \frac{f(x + h) - f(x)}{h} - \frac{h}{2}f^{^{\prime}}^{\prime}(\xi)

向后差商：f^{^{\prime}}(x) = \frac{f(x) - f(x - h)}{h} + \frac{h}{2}f^{^{\prime}}^{\prime}(\xi)

中心差商：f^{^{\prime}}(x) = \frac{f(x + h) - f(x - h)}{2}h - \frac{h^{2}}{6}f^{^{\prime}}^{\prime\prime}(\xi)

二阶中心差商：f^{^{\prime}}^{\prime}(x) = \frac{f(x + h) - 2f(x) + f(x - h)}{h^{2}} - \frac{h^{2}}{12}f^{(4)}(\xi)

Richardson 外推法求数值微分

\begin{array}{r} f(x + h) = f(x) + hf^{^{\prime}}(x) + \frac{h^{2}}{2}f^{^{\prime}}^{\prime}(x) + \frac{h^{3}}{6}f^{^{\prime}}^{\prime\prime}(x) + \ldots \\ f(x - h) = f(x) - hf^{^{\prime}}(x) + \frac{h^{2}}{2}f^{^{\prime}}^{\prime}(x) - \frac{h^{3}}{6}f^{^{\prime}}^{\prime\prime}(x) + \ldots \\ \Rightarrow f^{^{\prime}}(x) - \frac{f(x + h) - f(x - h)}{2h} = - \sum_{k = 1}^{\infty}\left( \frac{h^{2k}}{(2k + 1)!}f^{(2k + 1)}(x) \right) \end{array}

由 Richardson 外推法可构造递推公式：（其中$T(h)$为步长为$h$的一阶中心差商） $$\begin{cases} T_{0}(h) & = T(h) = \frac{f\left( x + \frac{h}{2} \right) - f\left( x - \frac{h}{2} \right)}{h} \\ T_{m}(h) & = \frac{4^{m}T_{m - 1}\left( \frac{h}{2} \right) - T_{m - 1}(h)}{4^{m} - 1} \end{cases}$$

利用数值积分做数值微分

$n$等分$\lbrack a,b\rbrack$，步长为$h = \frac{b - a}{n}$，则$f\left( x_{i + 1} \right) - f\left( x_{i - 1} \right) = \int_{x_{i - 1}}^{x_{i + 1}}f^{^{\prime}}(x)dx$，对右端采用不同的数值积分公式即得到不同的数值微分公式。

特征值

$$Ax = \lambda x$$

占优特征值与占优特征向量

如果$A$的某个特征值$\lambda_{i}$的量级远大于其他特征值，则称$\lambda_{i}$为占优特征值，对应的特征向量称为占优特征向量。

幂法

$$x^{T}Ax = x^{T}x\lambda \Longrightarrow \lambda = \frac{x^{T}Ax}{x^{T}x}$$

被成为 Rayleigh 商。给定特征向量近似，Rayleigh 商是最优近似。

具体方法：

1. 给定初始向量$x_{0}$

2. 迭代第$i$步：$u_{i - 1} = \frac{x_{i - 1}}{\| x_{i - 1}\|},\lambda_{i} = u_{i - 1}^{T}Au_{i - 1},x_{i} = Au_{i - 1}$

3. 最后得到的$u_{n} = \frac{x_{n}}{\| x_{n}\|}$即为最大特征值对应的特征向量。

对于几乎所有的初始向量，幂法都会线性收敛到最大特征值$\lambda_{1}$对应的特征向量，收敛常数为$|\frac{\lambda_{2}}{\lambda_{1}}|$。

反幂法与 Rayleigh 商迭代

$A^{- 1}$的最大特征值为$A$的最小特征值的倒数，将幂法应用于$A^{- 1}$即可得到$A$的最小特征值。但是注意避免求逆。

在求出最小特征值后，可以通过对$A - \lambda I$应用反幂法求出平移的特征向量。

若已知一个近似的特征值$\hat{\lambda}$，则$A - \hat{\lambda}$的最小特征值用反幂法可以很快求出，称为 Rayleigh 商迭代。

QR 方法：略

常微分方程

$$\begin{cases} y^{^{\prime}}(t) = f\left( t,y(t) \right) \\ y\left( t_{0} \right) = y_{0} \end{cases}$$

Lipschitz 条件

$\forall t \in \lbrack a,b\rbrack,y_{1},y_{2} \in R$ 有 $|f\left( t,y_{1} \right) - f\left( t,y_{2} \right)| \leq L|y_{1} - y_{2}|$

若$f(t,y)$定义在$\lbrack a,b\rbrack \times R$上且对$y$满足 Lipschitz 条件，则对任意初值问题在$\lbrack a,b\rbrack$上有唯一解。

适定性

若$f(t,y)$定义在$\lbrack a,b\rbrack \times R$上且对$y$满足 Lipschitz 条件，如果$Y(t)$和$Z(t)$分别具有初值条件$Y\left( t_{0} \right)$与$Z\left( t_{0} \right)$，则有$|Y(t) - Z(t)| \leq |Y\left( t_{0} \right) - Z\left( t_{0} \right)|\exp(L|t - t_{0}|)$

显式 Euler 方法

向前差分：$$f\left( t_{i},y_{i} \right) = y^{^{\prime}}\left( t_{i} \right) \approx \frac{y\left( t_{i + 1} \right) - y\left( t_{i} \right)}{h} \approx \frac{y_{i + 1} - y_{i}}{h} \Rightarrow y_{i + 1} = y_{i} + h \cdot f\left( t_{i},y_{i} \right)$$

稳定性：满足 Lipschitz 条件时，$|y_{i} - z_{i}| \leq |y_{0} - z_{0}|\exp(L|t_{i} - t_{0}|)$。

局部截断误差：（记M = \max|y^{^{\prime}}^{\prime}(t)|）\begin{aligned} \tau_{i + 1} = |y\left( t_{i + 1} \right) - y_{i + 1}| & = |y\left( t_{i} + h \right) - y\left( t_{i} \right) - hf\left( t_{i},y\left( t_{i} \right) \right)| \\ & = |hy^{^{\prime}}\left( t_{i} \right) + \frac{h^{2}}{2}y^{^{\prime}}^{\prime}(t) + \ldots - hy^{^{\prime}}\left( t_{i} \right)| \\ & = O\left( h^{2} \right) \leq \frac{M}{2}h^{2} \end{aligned}

称此方法具有一阶精度。

隐式 Euler 方法

向后差分：$$f\left( t_{i + 1},y_{i + 1} \right) = y^{^{\prime}}\left( t_{i + 1} \right) \approx \frac{y\left( t_{i + 1} \right) - y\left( t_{i} \right)}{h} \approx \frac{y_{i + 1} - y_{i}}{h} \Rightarrow y_{i + 1} = y_{i} + h \cdot f\left( t_{i + 1},y_{i + 1} \right)$$

由于只有$y_{i}$是给出的，因此需要求解非线性方程$F(x) = x - y_{i} - hf\left( t_{i + 1},x \right) = 0$，如牛顿法。

绝对稳定性：考虑$y^{^{\prime}}(t) = \lambda y(t)$，显式 Euler 方法的稳定性条件为$|1 + h\lambda| \leq 1$，隐式 Euler 方法的稳定性条件为$|1 - h\lambda| \geq 1$。

全局截断误差

满足 Lipschitz 条件时，单步 ODE 求解为$y_{i}$，局部截断误差$\tau_{i} \leq Ch^{k + 1}$，则求解器全局截断误差为$$e_{i} \leq \frac{Ch^{k}}{L}\left( \exp(L\left( t_{i} - t_{0} \right)) - 1 \right)$$ 因此局部截断误差为$O\left( h^{k + 1} \right)$的方法称为$k$阶方法。

梯形法

$$y_{i + 1} - y_{i} \approx \int_{t_{i}}^{t_{i + 1}}f\left( t,y(t) \right)dt \approx \frac{h}{2}\left( f\left( t_{i},y_{i} \right) + f\left( t_{i + 1},y_{i + 1} \right) \right)$$

隐式方法；二阶方法。

显式：先用显式 Euler 方法预测$y_{i + 1}$，再用梯形法迭代：$$y_{i + 1} = y_{i} + \frac{h}{2}\left( f\left( t_{i},y_{i} \right) + f\left( t_{i + 1},y_{i} + hf\left( t_{i},y_{i} \right) \right) \right)$$

也可以写成$$\begin{aligned} s_{1} & = f\left( t_{i},y_{i} \right) \\ s_{2} & = f\left( t_{i + 1},y_{i} + hs_{1} \right) \\ y_{i + 1} & = y_{i} + \frac{h}{2}\left( s_{1} + s_{2} \right) \end{aligned}$$

形如此类的方法称为二阶 Runge-Kutta 方法。

Runge-Kutta 方法

一般地，二阶显式 Runge-Kutta 方法为：$$\begin{aligned} s_{1} & = f\left( t_{i},y_{i} \right) \\ s_{2} & = f\left( t_{i} + ah,y_{i} + ahs_{1} \right) \\ y_{i + 1} & = y_{i} + h\left( b_{1}s_{1} + b_{2}s_{2} \right) \end{aligned}$$

显式梯形方法：$a = 1,b_{1} = b_{2} = \frac{1}{2}$

局部截断误差：略

• 一阶条件：$b_{1} + b_{2} = 1,\forall a$

• 二阶条件：$b_{1} + b_{2} = \frac{1}{2},ab_{2} = \frac{1}{2}$

• 三阶条件：不存在

中点法：$a = \frac{1}{2},b_{1} = 0,b_{2} = 1,y_{i + 1} = y_{i} + hf\left( t_{i} + \frac{h}{2},y_{i} + \frac{h}{2}f\left( t_{i},y_{i} \right) \right)$

更高阶的略

多步法

$$f\left( t_{i + 1},y_{i + 1} \right) = y^{^{\prime}}\left( t_{i + 1} \right) \approx \frac{y\left( t_{i + 2} \right) - y\left( t_{i} \right)}{2h} \approx \frac{y_{i + 2} - y_{i}}{2h} \Rightarrow y_{i + 2} = y_{i} + 2hf\left( t_{i + 1},y_{i + 1} \right)$$

初值条件为$y_{0},y_{1}$，两步法，二阶收敛。

一般地，初值条件给出$y_{0},y_{1},\ldots,y_{k - 1}$，$k$阶方法。 $$\sum_{j = 0}^{s}\alpha_{j}y_{i + j} = h\sum_{j = 0}^{s}\beta_{j}f\left( t_{i + j},y_{i + j} \right)$$

方程组与高阶方程

$$\begin{cases} y_{1}^{^{\prime}} = f_{1}\left( t,y_{1},y_{2},\ldots,y_{n} \right) \\ y_{2}^{^{\prime}} = f_{2}\left( t,y_{1},y_{2},\ldots,y_{n} \right) \\ \ldots \\ y_{n}^{^{\prime}} = f_{n}\left( t,y_{1},y_{2},\ldots,y_{n} \right) \end{cases}$$

每个变量都需要自己的初值。

对于高阶方程$y^{(n)} = f\left( t,y,y^{^{\prime}},\ldots,y^{(n - 1)} \right)$，可以引入新的变量$y_{1} = y,y_{2} = y^{^{\prime}},\ldots,y_{n} = y^{n - 1}$，转化为方程组$$\begin{cases} y_{1}^{^{\prime}} = y_{2} \\ y_{2}^{^{\prime}} = y_{3} \\ \ldots \\ y_{n - 1}^{^{\prime}} = y_{n} \\ y_{n}^{^{\prime}} = f\left( t,y_{1},y_{2},\ldots,y_{n} \right) \end{cases}$$