某凌溢的个人博客
item.title

最优化算法复习笔记

前置知识

  • 线性组合：对于一组向量 a1,…,ana_{1},\ldots,a_{n}，若存在一组标量 c1,…,cnc_{1},\ldots,c_{n} 使 a=∑ciaia = \sum c_{i}a_{i}，则称 aa 可由这组向量线性表示，且 c1,…,cnc_{1},\ldots,c_{n} 称为 aa 关于 a1,…,ana_{1},\ldots,a_{n} 的线性组合系数。

  • 线性相关、线性无关：对于一组向量，若能够由非全为零的系数线性表示为零向量则称为线性相关，否则称为线性无关。

  • 张成子空间：由一组向量线性组合得到的向量集合称为张成子空间。

  • 基、维数：若向量组线性无关且张成整个空间，则称为基，此向量组的向量个数称为维数。

  • 秩：矩阵的秩是指矩阵的列空间的维数。

    • 秩的其他定义：矩阵的行秩、列秩、左零空间、右零空间的维数……

  • 保秩运算：TODO

  • 矩阵的逆及其计算：若 AA 为可逆矩阵，则 A−1A^{- 1} 存在，且 AA−1=A−1A=IAA^{- 1} = A^{- 1}A = I。

    • 当矩阵的行列式不为零时，矩阵可逆。

  • 线性方程组 Ax=bAx = b 解的存在性理论：

  • 解的表达方式：

    • 齐次线性方程组的解：Ax=0Ax = 0 的解称为齐次线性方程组的解。

    • 非齐次线性方程组的解：Ax=bAx = b 的解称为非齐次线性方程组的解。

  • 范数：向量空间中的范数是一个函数，其满足非负性、齐次性、三角不等式

  • 内积：向量空间中的内积是一个函数，其满足对称性、线性性、正定性

  • 各种范数不等式：

    • 1-范数：∥x∥1=∑∣xi∣\| x\|_{1} = \sum|x_{i}|

    • 2-范数：∥x∥2=∑xi2\| x\|_{2} = \sqrt{\sum x_{i}^{2}}

    • 无穷范数：∥x∥∞=max⁡∣xi∣\| x\|_{\infty} = \max|x_{i}|

  • 线性变换：一个向量空间到另一个向量空间的映射，且满足线性性质（保持加法和数乘）。

    • 线性变换意义下的特征值：对于一个线性变换 TT，若存在一个非零向量 vv 使得 T(v)=λvT(v) = \lambda v，则称 λ\lambda 为 TT 的特征值，vv 为 TT 的特征向量。

  • 相似变换：若存在一个可逆矩阵 PP 使得 B=P−1APB = P^{- 1}AP，则称 AA 和 BB 相似。

  • 正交矩阵：若 ATA=IA^{T}A = I，则称 AA 为正交矩阵。

  • 对称矩阵：若 AT=AA^{T} = A，则称 AA 为对称矩阵。

  • 正交投影算子：TODO

  • 值域、零空间及其关系：

    • 值域：线性变换 TT 的值域是指所有 T(x)T(x) 的集合。

    • 零空间：线性变换 TT 的零空间是指所有 T(x)=0T(x) = 0 的集合。

    • 关系：值域和零空间的维数之和等于原空间的维数。

  • 正定二次型及其性质：若对于任意非零向量 xx，都有 xTAx>0x^{T}Ax > 0，则称 AA 为正定二次型。

  • 矩阵导出范数：对于给定的向量范数 ∥⋅∥\| \cdot \|，矩阵 AA 的导出范数定义为 ∥A∥=sup⁡x≠0∥Ax∥∥x∥=sup⁡∥x∥=1∥Ax∥\| A\| = \sup\limits_{x \neq 0}\frac{\| Ax\|}{\| x\|} = \sup\limits_{\| x\| = 1}\| Ax\|。

  • 瑞利不等式：对于一个对称矩阵 AA，有 λmin⁡≤xTAxxTx≤λmax⁡\lambda_{\min} \leq \frac{x^{T}Ax}{x^{T}x} \leq \lambda_{\max}。

线搜索

求解单峰的一元单值函数在闭区间上的最小值。

黄金分割法

将区间 [a,b]\lbrack a,b\rbrack 分成三份，切分点（比例）为 [0,λ,μ,1]\lbrack 0,\lambda,\mu,1\rbrack，其中 λ=1−μ\lambda = 1 - \mu，μ1=λμ\frac{\mu}{1} = \frac{\lambda}{\mu}，每次选择 [0,μ]\lbrack 0,\mu\rbrack 或 [λ,1]\lbrack\lambda,1\rbrack 作为新的区间，且只需要计算一个新的切分点。

计算可得 λ=5−12≈0.618\lambda = \frac{\sqrt{5} - 1}{2} \approx 0.618，μ=1−λ≈0.382\mu = 1 - \lambda \approx 0.382。

记第 kk 步时两侧区间的长度占比为 ρk\rho_{k}，那么满足 ρk+1(1−ρk)=1−2ρk\rho_{k + 1}\left( 1 - \rho_{k} \right) = 1 - 2\rho_{k} 时，其压缩率为 ∏1−ρk\prod 1 - \rho_{k}。当 ρk=3−52\rho_{k} = \frac{3 - \sqrt{5}}{2} 时，则为上面提到的黄金分割点，而若ρk=1−FN−k+1FN−k+2\rho_{k} = 1 - \frac{F_{N - k + 1}}{F_{N - k + 2}}（其中 FiF_{i} 为斐波那契数列）时，其压缩率为 1FN+1\frac{1}{F_{N + 1}}，总压缩比比黄金分割法更小。

二分法

将区间 [a,b]\lbrack a,b\rbrack 分成两份，每次选择中点 c=a+b2c = \frac{a + b}{2} 作为新的区间的一端，通过 f′(c)f^{\prime}(c) 的符号来确定新的区间。

需要一阶导数，每一步的压缩比为 12\frac{1}{2}。

牛顿法、割线法

二阶泰勒逼近：q(x)=f(xk)+f′(xk)(x−xk)+12f′′(xk)(x−xk)2q(x) = f\left( x_{k} \right) + f^{\prime}\left( x_{k} \right)\left( x - x_{k} \right) + \frac{1}{2}f^{\prime\prime}\left( x_{k} \right)\left( x - x_{k} \right)^{2}

取 q(x)q(x) 的极小值点作为下一个迭代点,即 q′(xk+1)=0‾⇒xk+1=xk−f′(xk)f′′(xk)\underline{q^{\prime}\left( x_{k + 1} \right) = 0} \Rightarrow x_{k + 1} = x_{k} - \frac{f^{\prime}\left( x_{k} \right)}{f^{\prime\prime}\left( x_{k} \right)}。

当 f′′(xk)>0f^{\prime\prime}\left( x_{k} \right) > 0 时，牛顿法可以正常运行；如果在一些点处 f′′(xk)<0‾\underline{f^{\prime\prime}\left( x_{k} \right) < 0}，则可能会出现收敛到极大点的情况。

割线法是牛顿法的一种变形，即用 f′′(xk)≈f′(xk)−f′(xk−1)xk−xk−1f^{\prime\prime}\left( x_{k} \right) \approx \frac{f^{\prime}\left( x_{k} \right) - f^{\prime}\left( x_{k - 1} \right)}{x_{k} - x_{k - 1}} 来代替二阶导数。此方法需要两个初始点，但只需要一阶导数。

这两种方法还可以用于计算 g(x)=0g(x) = 0 的根（q(xk+1)=0⇒xk+1=xk−g(xk)g′(xk)q\left( x_{k + 1} \right) = 0 \Rightarrow x_{k + 1} = x_{k} - \frac{g\left( x_{k} \right)}{g^{\prime}\left( x_{k} \right)}），也被称为牛顿割线法。

信赖域

TODO

无约束优化

通用格式：xk+1=xk+αkpkx_{k + 1} = x_{k} + \alpha_{k}p_{k}，其中 pkp_{k} 为搜索方向，αk\alpha_{k} 为步长。

梯度下降法

搜索方向：pk=−∇f(xk)p_{k} = - \nabla f\left( x_{k} \right)

最速下降法：αk= argminα≥0f(xk+αpk)\alpha_{k} = \text{ argmin}_{\alpha \geq 0}f\left( x_{k} + \alpha p_{k} \right)
对于最速下降法，只要 ∇f(xk)≠0\nabla f\left( x_{k} \right) \neq 0，则 f(xk+1)<f(xk)f\left( x_{k + 1} \right) < f\left( x_{k} \right)。

牛顿法

将 f:Rn→Rf:{\mathbb{R}}^{n} \rightarrow {\mathbb{R}} 在 xkx_{k} 处进行二阶泰勒展开，得到 q(x)=f(xk)+∇f(xk)⊤(x−xk)+12(x−xk)⊤H(xk)(x−xk)q(x) = f\left( x_{k} \right) + \nabla{f\left( x_{k} \right)}^{\top}\left( x - x_{k} \right) + \frac{1}{2}\left( x - x_{k} \right)^{\top}H\left( x_{k} \right)\left( x - x_{k} \right)，其中 H(xk)H\left( x_{k} \right) 为 ff 在 xkx_{k} 处的海森矩阵。若 H(xk)H\left( x_{k} \right) 正定，则 q(x)q(x) 有唯一极小值点，即 xk+1=xk−H(xk)−1∇f(xk)x_{k + 1} = x_{k} - {H\left( x_{k} \right)}^{- 1}\nabla f\left( x_{k} \right)

实际求解时，可以用 H(xk)pk=−∇f(xk)H\left( x_{k} \right)p_{k} = - \nabla f\left( x_{k} \right) 来求解 pkp_{k}，然后用 xk+1=xk+pkx_{k + 1} = x_{k} + p_{k} 来求解 xk+1x_{k + 1}。

共轭梯度法

共轭方向

QQ 是一个对称实矩阵，若 pi⊤Qpj=0(i≠j)p_{i}^{\top}Qp_{j} = 0(i \neq j)，则称 p1,…,pnp_{1},\ldots,p_{n} 为 QQ 关于 QQ 共轭。

克莱姆-施密特过程构造共轭方向

给定一组 Rn{\mathbb{R}}^{n} 的线性无关向量 a1,…,ana_{1},\ldots,a_{n}，可以通过以下过程得到一组关于对称正定矩阵 QQ 共轭的向量 p1,…,pnp_{1},\ldots,p_{n}：

  1. p1=a1p_{1} = a_{1}

  2. pk+1=ak+1−∑i=1k(ak+1⊤Qpi)pipi⊤Qpip_{k + 1} = a_{k + 1} - \sum_{i = 1}^{k}\left( a_{k + 1}^{\top}Qp_{i} \right)\frac{p_{i}}{p_{i}^{\top}Qp_{i}}

矩阵特征值分解构造共轭方向

若 QQ 为对称正定矩阵，且 Q=PΛP−1Q = P\Lambda P^{- 1}，则 pi=Peip_{i} = Pe_{i} 为 QQ 关于 QQ 共轭的向量。

共轭梯度法的步长与方向的推导

设 x∗−x0=∑i=0n−1βidix^{\ast} - x_{0} = \sum_{i = 0}^{n - 1}\beta_{i}d_{i}，两端同时乘以 dk⊤Qd_{k}^{\top}Q 可以得到 dk⊤Q(x∗−x0)=βkdk⊤Qdkd_{k}^{\top}Q\left( x^{\ast} - x_{0} \right) = \beta_{k}d_{k}^{\top}Qd_{k}（共轭的性质），因此 βk=dk⊤Q(x∗−x0)dk⊤Qdk\beta_{k} = \frac{d_{k}^{\top}Q\left( x^{\ast} - x_{0} \right)}{d_{k}^{\top}Qd_{k}}

考虑第 kk 步：x∗−x0=x∗−xk+(xk−x0)⇒dk⊤Q(x∗−x0)=dk⊤Q(x∗−xk)\begin{array}{r} x^{\ast} - x_{0} = x^{\ast} - x_{k} + \left( x_{k} - x_{0} \right) \\ \Rightarrow d_{k}^{\top}Q\left( x^{\ast} - x_{0} \right) = d_{k}^{\top}Q\left( x^{\ast} - x_{k} \right) \end{array}

由于 ∇f(x)=Qx−b\nabla f(x) = Qx - b，∇f(xk)=∇f(xk)−∇f(x∗)=Q(xk−x∗)\nabla f\left( x_{k} \right) = \nabla f\left( x_{k} \right) - \nabla f\left( x^{\ast} \right) = Q\left( x_{k} - x^{\ast} \right)，则综合这两个子式可以得到 dk⊤Q(x∗−x0)=dk⊤Q(x∗−xk)=dk⊤(−∇f(xk))d_{k}^{\top}Q\left( x^{\ast} - x_{0} \right) = d_{k}^{\top}Q\left( x^{\ast} - x_{k} \right) = d_{k}^{\top}\left( - \nabla f\left( x_{k} \right) \right)，即 βk=−dk⊤∇f(xk)dk⊤Qdk\beta_{k} = \frac{- d_{k}^{\top}\nabla f\left( x_{k} \right)}{d_{k}^{\top}Qd_{k}}

考虑到 dkd_{k} 一般通过迭代得到。dkd_{k} 需要满足 与之前的 did_{i} 宫娥 与 dk= span(dk−1,∇f(xk))d_{k} = \text{ span}\left( d_{k - 1},\nabla f\left( x_{k} \right) \right) 两个条件（后者的原因可能就是“共轭梯度法”这个名字的来源吧），因此设 dk=βkdk−1−∇f(xk)d_{k} = \beta_{k}d_{k - 1} - \nabla f\left( x_{k} \right)，因为共轭，有 dk−1⊤Qdk=βkdk−1⊤Qdk−1−dk−1⊤Q∇f(xk)⇒βk=…d_{k - 1}^{\top}Qd_{k} = \beta_{k}d_{k - 1}^{\top}Qd_{k - 1} - d_{k - 1}^{\top}Q\nabla f\left( x_{k} \right) \Rightarrow \beta_{k} = \ldots

拟牛顿法

在牛顿法中 xk=xk−1−H(xk−1)−1∇f(xk−1)x_{k} = x_{k - 1} - {H\left( x_{k - 1} \right)}^{- 1}\nabla f\left( x_{k - 1} \right) 中，每一步都要计算 H(xk−1)−1{H\left( x_{k - 1} \right)}^{- 1}，而拟牛顿法通过近似 H(xk−1)H\left( x_{k - 1} \right) 或者它的逆来减少计算量，即 Bk≈H(xk−1)B_{k} \approx H\left( x_{k - 1} \right) 或 Hk≈H(xk−1)−1H_{k} \approx {H\left( x_{k - 1} \right)}^{- 1}。

f′′(xk)≈f′(xk)−f′(xk−1)xk−xk−1⇒f′(xk−1)≈f′(xk)+f′′(xk)(xk−1−xk)f^{\prime\prime}\left( x_{k} \right) \approx \frac{f^{\prime}\left( x_{k} \right) - f^{\prime}\left( x_{k - 1} \right)}{x_{k} - x_{k - 1}} \Rightarrow f^{\prime}\left( x_{k - 1} \right) \approx f^{\prime}\left( x_{k} \right) + f^{\prime\prime}\left( x_{k} \right)\left( x_{k - 1} - x_{k} \right)

记 Δgk=∇f(xk−1)−∇f(xk),Δxk=xk−1−xk\Delta g_{k} = \nabla f\left( x_{k - 1} \right) - \nabla f\left( x_{k} \right),\Delta x_{k} = x_{k - 1} - x_{k}（好扭曲的符号……），则上式简记为 (∇2f(xk))−1Δgk−1=Δxk−1\left( \nabla^{2}f\left( x_{k} \right) \right)^{- 1}\Delta g_{k - 1} = \Delta x_{k - 1}，即 HkΔgk−1=Δxk−1H_{k}\Delta g_{k - 1} = \Delta x_{k - 1}。

通常希望 HkH_{k} 满足：对称正定、迭代计算量少、近似效果好。

SR1

{Hk+1Δgk=ΔxHk+1=Hk+auu⊤\begin{cases} H_{k + 1}\Delta g_{k} = \Delta x \\ H_{k + 1} = H_{k} + auu^{\top} \end{cases}

代入得 (Hk+auu⊤)Δgk=Δxk=HkΔgk+auu⊤Δgk\left( H_{k} + auu^{\top} \right)\Delta g_{k} = \Delta x_{k} = H_{k}\Delta g_{k} + auu^{\top}\Delta g_{k}，即 au⊤Δgku=Δxku−HkΔgkuau^{\top}\Delta g_{k}u = \Delta x_{k}u - H_{k}\Delta g_{k}u。注意到 au⊤Δgkau^{\top}\Delta g_{k} 是一个标量，不妨让它等于 11，则 uu 与 aa 依次可以解出。

公式太长，这里不放。

DFP

思想和上面类似，只不过变成了秩二修正，即 Hk+1=Hk+auu⊤+bvv⊤H_{k + 1} = H_{k} + auu^{\top} + bvv^{\top}。

同样代入得到 au⊤Δgku+bv⊤Δgkv=Δxk−HkΔgkau^{\top}\Delta g_{k}u + bv^{\top}\Delta g_{k}v = \Delta x_{k} - H_{k}\Delta g_{k}

一个简单的解为 u=Δxk,v=HkΔgku = \Delta x_{k},v = H_{k}\Delta g_{k}。

公式太长，还是不放。

BFGS

思想和上面类似，只不过变成了估计 ∇2f(xk)\nabla^{2}f\left( x_{k} \right)，即 Bk+1=Bk+auu⊤+bvv⊤B_{k + 1} = B_{k} + auu^{\top} + bvv^{\top}。

这下代入的应该是 BkΔxk=ΔgkB_{k}\Delta x_{k} = \Delta g_{k} 了，即 au⊤Δxku+bv⊤Δxkv=Δgk−BkΔxkau^{\top}\Delta x_{k}u + bv^{\top}\Delta x_{k}v = \Delta g_{k} - B_{k}\Delta x_{k}

与 DFP 非常对称。

Sherman-Morrison 公式

对于一个矩阵 AA，若 A+uv⊤A + uv^{\top} 可逆，则有 (A+uv⊤)−1=A−1−A−1uv⊤A−11+v⊤A−1u\left( A + uv^{\top} \right)^{- 1} = A^{- 1} - \frac{A^{- 1}uv^{\top}A^{- 1}}{1 + v^{\top}A^{- 1}u}。

线性规划

标准型与松弛

 minimize c⊤xs.t. Ax=b≥0x≥0\begin{aligned} \text{ minimize } & c^{\top}x \\ \text{s.t. } & Ax = b \geq 0 \\ & x \geq 0 \end{aligned}

化标准型方法：

  • max⁡f(x)⇒min⁡−f(x)\max f(x) \Rightarrow \min - f(x)

  • x≤c⇒x+x′=c,x′≥0x \leq c \Rightarrow x + x^{\prime} = c,x^{\prime} \geq 0 （松弛）

  • ax=b<0⇒−ax=−bax = b < 0 \Rightarrow - ax = - b

  • x∈R⇒x=x′−x′′,x′,x′′≥0x \in {\mathbb{R}} \Rightarrow x = x^{\prime} - x^{\prime\prime},x^{\prime},x^{\prime\prime} \geq 0 （非负拆分）

设A∈Rm×nA \in {\mathbb{R}}_{m \times n}，其中m<nm < n，于是进行列重排，使得A=[B,D],B∈Rm×mA = \lbrack B,D\rbrack,B \in {\mathbb{R}}_{m \times m}，于是存在一个解 x⊤=[B−1b;0]x^{\top} = \left\lbrack B^{- 1}b;0 \right\rbrack，被称为基本解； BB 的列被称为基本列，xB=B−1bx_{B} = B^{- 1}b 被称为基本变量。

注：若 xBx_{B} 中有零值，则被称为退化的基本解。若某个可行解为（退化的）基本解，则称为（退化的）基本可行解。

单纯形法

基本思想：从一个基本可行解出发，通过改变基本变量，使得目标函数值逐渐减小，直到找到最优解。

当将 AA 划分为 [B ∣ D]\left\lbrack B~|~D \right\rbrack 后，目标函数值就可以表达为 z=cB⊤B−1b+(cD⊤−cB⊤B−1D)xDz = c_{B}^{\top}B^{- 1}b + \left( c_{D}^{\top} - c_{B}^{\top}B^{- 1}D \right)x_{D}，其中定义 rD=cD⊤−cB⊤B−1Dr_{D} = c_{D}^{\top} - c_{B}^{\top}B^{- 1}D。由于 x≥0x \geq 0，因此若 rD≥0r_{D} \geq 0，则有最优解 x=[B−1b;0]x = \left\lbrack B^{- 1}b;0 \right\rbrack，否则将 rDr_{D} 中的一个负值对应的列加入基本列，然后通过高斯消元法来求解新的基本解。

单纯形法的矩阵形式

(BDbcB⊤cD⊤0)⇒(IB−1DB−1b0cD⊤−cB⊤B−1D−cB⊤B−1b)=(IB−1DB−1b0rD⊤−z0)\begin{pmatrix} B & D & b \\ c_{B}^{\top} & c_{D}^{\top} & 0 \end{pmatrix} \Rightarrow \begin{pmatrix} I & B^{- 1}D & B^{- 1}b \\ 0 & c_{D}^{\top} - c_{B}^{\top}B^{- 1}D & - c_{B}^{\top}B^{- 1}b \end{pmatrix} = \begin{pmatrix} I & B^{- 1}D & B^{- 1}b \\ 0 & r_{D}^{\top} & - z_{0} \end{pmatrix}

  • 若 rD≥0r_{D} \geq 0，则找到最优解 x=[B−1b;0]x = \left\lbrack B^{- 1}b;0 \right\rbrack，此时 z=z0z = z_{0}

  • 否则，选择最小的 rDr_{D} 中的元素 rDjr_{D_{j}}，然后进行转轴运算。

转轴元素的选取

在选好列 ll 后，由于 bi′=bi−bkaklailb^{\prime}_{i} = b_{i} - \frac{b_{k}}{a_{kl}}a_{il}，所以希望 bkakl\frac{b_{k}}{a_{k_{l}}} 最小。

初始解的选择——二阶段法

min⁡c⊤x⇒min⁡y1+…+ym\min c^{\top}x \Rightarrow \min y_{1} + \ldots + y_{m} [A ∣ I][x;y]=b,x,y≥0\left\lbrack A~|~I \right\rbrack\lbrack x;y\rbrack = b,x,y \geq 0

  • 若这个问题的最优解对应函数值为 z>0z > 0，则原问题无解

  • 若解中存在 yi>0y_{i} > 0，则

    • 若 yiy_{i} 所在行的 AA 部分的所有元素均为零，则 yiy_{i} 为冗余约束，可以将其去掉

    • 否则以任意一个非零的 yiy_{i} 所在行的 AA 部分的元素进行转轴操作

  • 若解中不存在 yi>0y_{i} > 0，则将 yiy_{i} 所在列删去，直至得到一个原问题的基本可行解，此时再替换 cc

大 M 法

{min⁡c⊤xAx=bx≥0⇒{min⁡c⊤x+M∑yiAx+y‾=bx,y≥0\begin{cases} \min c^{\top}x \\ Ax = b \\ x \geq 0 \end{cases} \Rightarrow \begin{cases} \min c^{\top}x + M\sum y_{i} \\ Ax\underline{+ y} = b \\ x,y \geq 0 \end{cases}

将 MM 代入一个无穷大的数处理即可。

具体在应用这些方法时，只需要能够构造出可行解即可，即：在 AA 中有只包含 1 个 11 的列时，不需要严格构造 mm 个 yy。

整数规划

割平面法

原理：通过增加约束条件，把由单纯形法得到的非整数解从可行集中去除掉。新增的约束条件不去除可行集中的整数解。不断增加约束条件，直到得到一个整数最优解。

分支定界法

原理：将整数规划问题松弛，若解包含非整数分量 xi=x∗x_{i} = x^{\ast}，则分为两个问题：xi≤⌊x∗⌋x_{i} \leq \left\lfloor x^{\ast} \right\rfloor 与 xi≥⌊x∗⌋+1x_{i} \geq \left\lfloor x^{\ast} \right\rfloor + 1，然后递归求解。

约束优化

等式约束

min⁡f(x) s.t. h(x)=0\min f(x)\quad\text{ s.t. }h(x) = 0

其中 x∈Rn,f:Rn→R,h:Rn→Rm,m≤nx \in {\mathbb{R}}^{n},f:{\mathbb{R}}^{n} \rightarrow {\mathbb{R}},h:{\mathbb{R}}^{n} \rightarrow {\mathbb{R}}^{m},m \leq n

正则点：若 hi(x∗)=0,∇hi(x∗)h_{i\left( x^{\ast} \right)} = 0,\nabla h_{i}\left( x^{\ast} \right) 线性无关，则 x∗x^{\ast} 为正则点。x∗x^{\ast} 为正则点 ⇔R(∇h(x∗))=m\Leftrightarrow R\left( \nabla h\left( x^{\ast} \right) \right) = m

切线空间 T(x∗)={y:∇h(x∗)⊤y=0}T\left( x^{\ast} \right) = \left\{ y:\nabla{h\left( x^{\ast} \right)}^{\top}y = 0 \right\}，法线空间 N(x∗)= span(∇h(x∗))N\left( x^{\ast} \right) = \text{ span}\left( \nabla h\left( x^{\ast} \right) \right)

Lagrange 函数

选择点 x∗x^{\ast} 使得 h(x∗)=0,∇h(x∗)≠0h\left( x^{\ast} \right) = 0,\nabla h\left( x^{\ast} \right) \neq 0，过 x∗x^{\ast} 的水平集 x(t),t∈(a,b)x(t),t \in (a,b) 有 x∗=x(t∗),∀t,h(x(t))=0x^{\ast} = x\left( t^{\ast} \right),\forall t,h\left( x(t) \right) = 0，则 ddth(x(t))=(∇h(x))⊤x˙(t)=0\frac{d}{dt}h\left( x(t) \right) = \left( \nabla h(x) \right)^{\top}\dot{x}(t) = 0。若 x∗x^{\ast} 为 f(x)f(x) 在 {x:h(x)=0}\left\{ x:h(x) = 0 \right\} 上的极小点，则同理可得 ∇f(x∗)\nabla f\left( x^{\ast} \right) 与 x˙(t)\dot{x}(t) 也正交。

（一阶必要条件）综上：若 x∗x^{\ast} 为等式约束的极值点，则 ∇f(x∗)\nabla f\left( x^{\ast} \right) 与 ∇h(x∗)\nabla h\left( x^{\ast} \right) 平行，即 ∃λ∗ s.t. ∇f(x∗)+(λ∗)⊤∇h(x∗)=0,h(x∗)=0\exists\lambda^{\ast}\text{ s.t. }\nabla f\left( x^{\ast} \right) + \left( \lambda^{\ast} \right)^{\top}\nabla h\left( x^{\ast} \right) = 0,\quad h\left( x^{\ast} \right) = 0

（Lagrange 函数）定义 l(x;λ)=f(x)+λ⊤h(x)l(x;\lambda) = f(x) + \lambda^{\top}h(x) 则一阶的两个必要条件可以写成 ∇l(x∗;λ∗)=0\nabla l\left( x^{\ast};\lambda^{\ast} \right) = 0

（二阶必要条件）若正则点 x∗x^{\ast} 为等式约束的极小点，则存在 λ∗\lambda^{\ast} 使得一阶条件满足且 ∇2l(x∗;λ∗)\nabla^{2}l\left( x^{\ast};\lambda^{\ast} \right) 在切线空间 T(x∗)T\left( x^{\ast} \right) 上半正定（∀y∈T(x∗),y⊤∇2l(x∗;λ∗)y≥0\forall y \in T\left( x^{\ast} \right),y^{\top}\nabla^{2}l\left( x^{\ast};\lambda^{\ast} \right)y \geq 0）

不等式约束

min⁡f(x) s.t. h(x)=0,g(x)≤0\min f(x)\quad\text{ s.t. }h(x) = 0,g(x) \leq 0

其中 x∈Rn,f:Rn→R,h:Rn→Rm,g:Rn→Rp,m≤nx \in {\mathbb{R}}^{n},f:{\mathbb{R}}^{n} \rightarrow {\mathbb{R}},h:{\mathbb{R}}^{n} \rightarrow {\mathbb{R}}^{m},g:{\mathbb{R}}^{n} \rightarrow {\mathbb{R}}^{p},m \leq n

积极/非积极约束、正则点

对于一个不等式约束 gi(x)≤0g_{i}(x) \leq 0，若在 x∗x^{\ast} 处 gi(x∗)=0g_{i}\left( x^{\ast} \right) = 0，则称 gi(x∗)g_{i}\left( x^{\ast} \right) 为积极约束；若 gi(x∗)<0g_{i}\left( x^{\ast} \right) < 0，则称 gi(x∗)g_{i}\left( x^{\ast} \right) 为非积极约束。

等式约束总是积极约束。

若 x∗x^{\ast} 满足所有约束条件 J(x∗)≜{j:gj(x∗)=0}J\left( x^{\ast} \right) \triangleq \left\{ j:g_{j}\left( x^{\ast} \right) = 0 \right\} 如果 ∇hi(x∗),∇gj(x∗),1≤j≤m,j∈J(x∗)\nabla h_{i}\left( x^{\ast} \right),\nabla g_{j}\left( x^{\ast} \right),1 \leq j \leq m,j \in J\left( x^{\ast} \right) （所有积极约束）线性无关，则称 x∗x^{\ast} 为正则点。

KKT 条件

min⁡f(x) s.t. h(x)=0,g(x)≤0\min f(x)\quad\text{ s.t. }h(x) = 0,g(x) \leq 0

  1. 原始可行性：h(x∗)=0,g(x∗)≤0h\left( x^{\ast} \right) = 0,g\left( x^{\ast} \right) \leq 0

  2. 对偶可行性：μ∗≥0\mu^{\ast} \geq 0

  3. 互补松弛条件：μ∗g(x∗)=0\mu^{\ast}g\left( x^{\ast} \right) = 0

  4. 原始最优性：∇f(x∗)+(λ∗)⊤∇h(x∗)+(μ∗)⊤∇g(x∗)=0\nabla f\left( x^{\ast} \right) + \left( \lambda^{\ast} \right)^{\top}\nabla h\left( x^{\ast} \right) + \left( \mu^{\ast} \right)^{\top}\nabla g\left( x^{\ast} \right) = 0

注意 μ⋛0\mu \gtreqless 0 与 g(x)⋛0g(x) \gtreqless 0

对偶可行性

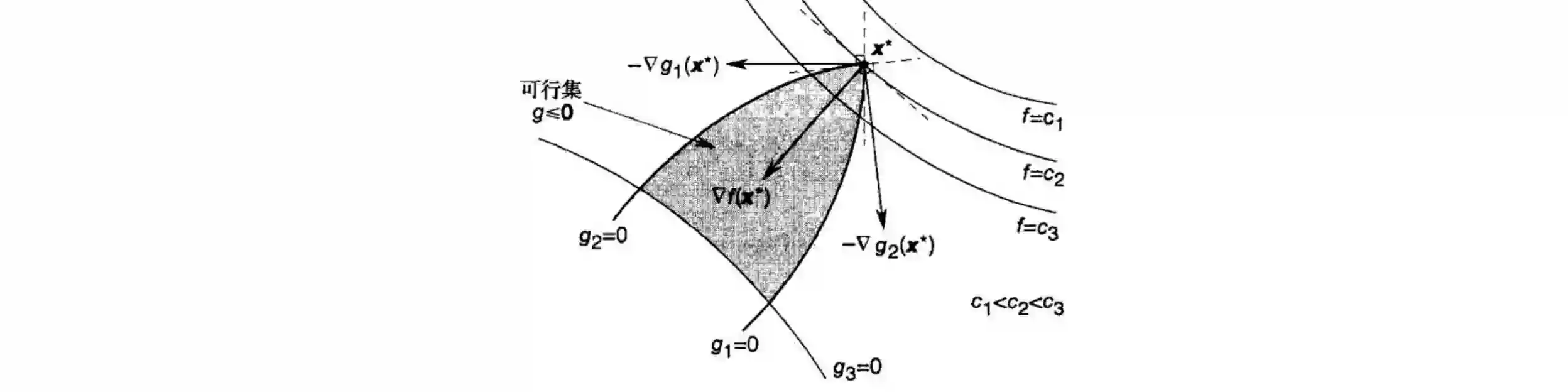
当约束条件为 gj(x)≤0g_{j(x)} \leq 0 时，可行集的方向为 −∇gj(x)- \nabla g_{j}(x)，因此要使得 x∗x^{\ast} 为最优解，需要 ∇f(x∗)=−∑μj∗∇gj(x∗),μ∗≥0\nabla f\left( x^{\ast} \right) = - \sum\mu_{j}^{\ast}\nabla g_{j}\left( x^{\ast} \right),\mu^{\ast} \geq 0

互补松弛条件

μjgj(x∗)=0\mu_{j}g_{j}\left( x^{\ast} \right) = 0 说明了对于每个约束：

  • 若为积极约束，则约束体现在原始最优性中

  • 若为非积极约束，此约束不应该对最优解产生影响（即不约束 ∇f(x∗)\nabla f\left( x^{\ast} \right) 的方向）

二阶必要条件

L(x,λ,μ)=∇2f(x)+λ⊤∇2h(x)+μ⊤∇2g(x)L(x,\lambda,\mu) = \nabla^{2}f(x) + \lambda^{\top}\nabla^{2}h(x) + \mu^{\top}\nabla^{2}g(x)

若 x∗x^{\ast} 为正则点，则极小值的二阶必要条件为：存在 λ∗,μ∗\lambda^{\ast},\mu^{\ast} 使得在满足一阶 KKT 条件的情况下，对于所有 y∈T(x∗)y \in T\left( x^{\ast} \right) 有 y⊤L(x∗,λ∗,μ∗)y≥0y^{\top}L\left( x^{\ast},\lambda^{\ast},\mu^{\ast} \right)y \geq 0

拉格朗日对偶

l(x;λ,μ)=f(x)+λ⊤h(x)+μ⊤g(x)l(x;\lambda,\mu) = f(x) + \lambda^{\top}h(x) + \mu^{\top}g(x)

原问题为 min⁡f(x) s.t. h(x)=0,g(x)≤0\min f(x)\quad\text{ s.t. }h(x) = 0,g(x) \leq 0，因此 l(x;λ,μ)≤f(x)l(x;\lambda,\mu) \leq f(x)，代入最优解 x∗x^{\ast} 有 l(x∗;λ∗,μ∗)≤f(x∗)l\left( x^{\ast};\lambda^{\ast},\mu^{\ast} \right) \leq f\left( x^{\ast} \right)，自然有 max⁡l(x∗;λ∗,μ∗)≤f(x∗)\max l\left( x^{\ast};\lambda^{\ast},\mu^{\ast} \right) \leq f\left( x^{\ast} \right)，因此可以定义拉格朗日对偶函数 g(λ,μ)=max⁡l(x;λ,μ)g(\lambda,\mu) = \max l(x;\lambda,\mu)

弱对偶性

由上面的推导可知，g(λ∗,μ∗)≤f(x∗)g\left( \lambda^{\ast},\mu^{\ast} \right) \leq f\left( x^{\ast} \right)，这被称为弱对偶性。

最大值中的最小值大于等于最小值中的最大值

强对偶性

若可行解 x∗,λ∗,μ∗x^{\ast},\lambda^{\ast},\mu^{\ast} 满足 g(λ∗,μ∗)=f(x∗)g\left( \lambda^{\ast},\mu^{\ast} \right) = f\left( x^{\ast} \right)，则 x∗x^{\ast} 为原问题的最优解，λ∗,μ∗\lambda^{\ast},\mu^{\ast} 为对偶问题的最优解，这被称为强对偶性。

拉格朗日函数 l(x;λ,μ)l(x;\lambda,\mu) 存在鞍点当且仅当强对偶性成立。

Slater 条件：若存在一个 xx 使得 h(x)=0,g(x)<0h(x) = 0,g(x) < 0，则强对偶性成立。（反之不一定成立）

线性规划的例子

min⁡c⊤xs.t. Ax=b,x≥0\begin{array}{r} \min c^{\top}x \\ \text{s.t. }Ax = b,x \geq 0 \end{array}

得到 l(x;λ)=c⊤x+λ⊤(Ax−b)l(x;\lambda) = c^{\top}x + \lambda^{\top}(Ax - b)，原始问题为 min⁡xmax⁡λl(x;λ)\min\limits_{x}\max\limits_{\lambda}l(x;\lambda)，对偶问题为 max⁡λmin⁡xl(x;λ)\max\limits_{\lambda}\min\limits_{x}l(x;\lambda)。令 g(λ)=min⁡xl(x;λ)=min⁡x((c⊤+λ⊤A)x−λ⊤b)g(\lambda) = \min\limits_{x}l(x;\lambda) = \min\limits_{x}\left( \left( c^{\top} + \lambda^{\top}A \right)x - \lambda^{\top}b \right) 则对偶问题为 max⁡λg(λ)\max\limits_{\lambda}g(\lambda)。

因为 x≥0x \geq 0，所以如果 c⊤+λ⊤Ac^{\top} + \lambda^{\top}A 的某个分量为负，则 g(λ)g(\lambda) 可以取到 −∞- \infty；因此需要 c⊤+λ⊤A≥0c^{\top} + \lambda^{\top}A \geq 0，此时 g(λ)=−λ⊤bg(\lambda) = - \lambda^{\top}b，因此对偶问题为 max⁡λ−λ⊤b s.t. c⊤≥−λ⊤A\max\limits_{\lambda} - \lambda^{\top}b\quad\text{ s.t. }c^{\top} \geq - \lambda^{\top}A

或：min⁡λλ⊤b s.t. λ⊤A≤c\min\limits_{\lambda}\lambda^{\top}b\text{ s.t. }\lambda^{\top}A \leq c

凸优化

  • 函数图像：epi(f)={[x;t]:x∈Ω,t≥f(x)}\text{epi}(f) = \left\{ \lbrack x;t\rbrack:x \in \Omega,t \geq f(x) \right\}

  • 凸函数：若 epi(f)\text{epi}(f) 为凸集，则称 ff 为凸函数

  • 凸集：若对于任意 x,y∈C,0≤λ≤1x,y \in C,0 \leq \lambda \leq 1，有 λx+(1−λ)y∈C\lambda x + (1 - \lambda)y \in C，则称 CC 为凸集

  • 广义梯度：对于凸函数 ff，定义 ∇f(x)={g:f(y)≥f(x)+g⊤(y−x),∀y}\nabla f(x) = \left\{ g:f(y) \geq f(x) + g^{\top}(y - x),\forall y \right\}（在 xx 处能够“包住”整个函数的切线集合，类似全空间减去一个椎体）

    • 定义在开凸集上的二阶连续函数：凸函数 ⇔\Leftrightarrow ∇2f(x)\nabla^{2}f(x) 半正定（凹函数：半负定）

  • 保凸性质：线性组合、求上确界……

凸优化问题的性质

  • 局部最优解 ⇔\Leftrightarrow 全局最优解

  • 全局极小条件：若 x∗x^{\ast} 满足对任意可行方向 dd，有 d⊤∇f(x∗)≥0d^{\top}\nabla f\left( x^{\ast} \right) \geq 0，则 x∗x^{\ast} 为全局极小点

  • 拉格朗日条件、KKT 条件在凸优化问题中是充分条件

投影方法

约束问题 min⁡f(x) s.t. x∈Ω\min f(x)\text{ s.t. }x \in \Omega 用无约束优化迭代格式 xk+1=xk+αkdkx_{k + 1} = x_{k} + \alpha_{k}d_{k} 来求解可能会导致迭代点不在可行域内，因此需要投影方法来保证迭代点在可行域内。

投影：设 Ω\Omega 为非空闭凸集，∀x∈Rn\forall x \in {\mathbb{R}}^{n}，定义其在 Ω\Omega 上的投影为 ∏(x)= argminz∈Ω∥x−z∥\prod(x) = \text{ argmin}_{z \in \Omega}\| x - z\|

  • Ω\Omega 为非空闭凸集时，投影存在且唯一

  • 投影是非扩张的：∥∏(x)−∏(y)∥≤∥x−y∥\|\prod(x) - \prod(y)\| \leq \| x - y\|

投影方法：xk+1=∏(xk+αkdk)x_{k + 1} = \prod(x_{k} + \alpha_{k}d_{k})

简单集合的投影表达式

  • 箱形约束：Ω={x∈Rn:l≤x≤u}\Omega = \left\{ x \in {\mathbb{R}}^{n}:l \leq x \leq u \right\}，则 ∏(x)= median(l,x,u)\prod(x) = \text{ median}(l,x,u)

  • 球形约束：Ω={x∈Rn:∥x∥≤r}\Omega = \left\{ x \in {\mathbb{R}}^{n}:\| x\| \leq r \right\}，则 ∏(x)=min⁡(1,r∥x∥)x\prod(x) = \min(1,\frac{r}{\| x\|})x

拉格朗日法

约束问题 min⁡f(x) s.t. h(x)=0,g(x)≤0\min f(x)\text{ s.t. }h(x) = 0,g(x) \leq 0 的拉格朗日函数为 l(x;λ,μ)=f(x)+λ⊤h(x)+μ⊤g(x)l(x;\lambda,\mu) = f(x) + \lambda^{\top}h(x) + \mu^{\top}g(x)

xk+1=xk−αk∇xl(xk;λk,μk)λk+1=λk+βkh(xk)μk+1=[μk+γkg(xk)]+\begin{array}{r} x_{k + 1} = x_{k} - \alpha_{k}\nabla_{x}l\left( x_{k};\lambda_{k},\mu_{k} \right) \\ \lambda_{k + 1} = \lambda_{k} + \beta_{k}h\left( x_{k} \right) \\ \mu_{k + 1} = \left\lbrack \mu_{k} + \gamma_{k}g\left( x_{k} \right) \right\rbrack_{+} \end{array}

罚函数法

约束问题 min⁡f(x) s.t. x∈Ω\min f(x)\text{ s.t. }x \in \Omega 等价于无约束问题 min⁡f(x)+ιΩ(x)\min f(x) + \iota_{\Omega}(x)，其中 ιΩ(x)\iota_{\Omega}(x) 为指示函数，定义为 ιΩ(x)={0, if x∈Ω+∞, otherwise\iota_{\Omega}(x) = \begin{cases} 0, & \quad\text{ if }x \in \Omega \\ + \infty, & \quad\text{ otherwise} \end{cases}

一般使用 γP(x)\gamma P(x) 近似指示函数，其中 γ\gamma 称为罚因子，P(x)P(x) 称为罚函数。

罚函数一般满足：

  • 连续

  • P(x)=0⇔x∈ΩP(x) = 0 \Leftrightarrow x \in \Omega

  • P(x)≥0P(x) \geq 0

约束优化的罚函数：

  • 精确罚函数：P(x)=∣h(x)∣+∣g+(x)∣P(x) = |h(x)| + |g^{+ (x)}|

  • 二次罚函数：P(x)=∥h(x)∥2+∥g+(x)∥2P(x) = \| h(x)\|^{2} + \| g^{+ (x)}\|^{2}

增广拉格朗日法

相当于 min⁡f(x)+γ(∥h(x)∥2+∥g+(x)∥2) s.t. h(x)=0,g(x)≤0\min f(x) + \gamma(\| h(x)\|^{2} + \| g^{+ (x)}\|^{2})\text{ s.t. }h(x) = 0,g(x) \leq 0

增广拉格朗日函数：l(x;λ,μ,γ)=f(x)+λ⊤h(x)+μ⊤g(x)+γ(∥h(x)∥2+∥g+(x)∥2),μ≥0l(x;\lambda,\mu,\gamma) = f(x) + \lambda^{\top}h(x) + \mu^{\top}g(x) + \gamma(\| h(x)\|^{2} + \| g^{+ (x)}\|^{2}),\mu \geq 0

迭代格式：

  1. xk+1= argminxl(x;λk,μk,γ)x_{k + 1} = \text{ argmin}_{x}l\left( x;\lambda_{k},\mu_{k},\gamma \right)

  2. λk+1=λk+γh(xk)\lambda_{k + 1} = \lambda_{k} + \gamma h\left( x_{k} \right)

  3. μk+1=[μk+γg+(xk)]+\mu_{k + 1} = \left\lbrack \mu_{k} + \gamma g^{+ \left( x_{k} \right)} \right\rbrack_{+}

多目标优化（了解）

多目标优化：具有多个目标函数的优化问题，通常是多个目标函数之间存在矛盾，无法同时优化。

Pareto 最优解

定义：若 x∗x^{\ast} 为 Pareto 最优解，则不存在 xx 使得 f(x)≤f(x∗)f(x) \leq f\left( x^{\ast} \right) 且 f(x)≠f(x∗)f(x) \neq f\left( x^{\ast} \right)。

求解过程：维护一个 Pareto 集合，对任意候选解：

  • 若其受到 Pareto 集合中某个解的支配，则舍弃

  • 若其支配 Pareto 集合中某个解，则删除被支配的解，且加入该解

  • 否则加入 Pareto 集合

转换为单目标优化

  • 线性加权法：f′(x)=c⊤f(x),c>0f^{\prime}(x) = c^{\top}f(x),c > 0，但是 cc 的选择是一个问题

  • 极小极大法：f′(x)=max⁡ifi(x)f^{\prime}(x) = \max\limits_{i}f_{i}(x)，但是分量函数需要兼容（即：单位一致），且可能f′(x)f^{\prime}(x)不可微分

  • 范数法：若目标向量全部非负，则 f′(x)=∥f(x)∥2f^{\prime}(x) = \| f(x)\|_{2}

  • 转化为约束问题：选择一个 ii，问题转化为 min⁡fi(x) s.t. ∀j≠i,fj(x)≤bj\min f_{i}(x)\text{ s.t. }\forall j \neq i,f_{j}(x) \leq b_{j}，需要先确定一个期望

unimplemented: 不确定的线性规划