概率论与数理统计复习笔记

随机事件和概率

随机事件

随机试验和随机事件

随机试验的特征：可重复性、结果明确性、不可预测性

随机事件：在一定条件下基于一定的试验目的进行试验，称试验中每一个可能发生也可能不发生的事情为随机事件，简称事件，用大写字母$A,B,C,\ldots$表示。

• 基本事件：在一次试验中必发生一个且仅发生一个的最简单事件

• 复合事件：由若干基本事件组合而成的事件

若试验目的不同，则基本事件也可能不同。

必然事件记为 $\Omega$，不可能事件记为 $\varnothing$。

集合表示

基本事件对应一个单点集，所有基本事件 $A_{n}$ 对应的单点集 $\left\{ \omega_{n} \right\}$ 的并集为样本空间 $\Omega = \left\{ \omega_{1},\omega_{2},\ldots,\omega_{n} \right\}$，其中的每一个元素称为样本点。

若试验目的不同，基本事件可能不同，样本空间因此也可能不同。

集合运算

中心思想：若一次试验的结果 $\omega \in A$，则称事件 $A$ 发生，否则称事件 $A$ 不发生。

• 事件的和：$A \cup B = \left\{ \omega~|~\omega \in A\text{ or }\omega \in B \right\}$

• 事件的交：$A \cap B(AB) = \left\{ \omega~|~\omega \in A\text{ and }\omega \in B \right\}$

• 事件的差：$A - B = \left\{ \omega~|~\omega \in A\text{ and }\omega \notin B \right\}$

事件的关系

• 包含：$A \subset B$

• 互不相容：$AB = \varnothing$

• 对立事件：$AB = \varnothing\text{ and }A \cup B = \Omega$（记为 $B = \overline{A}$ ）

事件的运算律

• 交换律：$A \cup B = B \cup A,A \cap B = B \cap A$

• 结合律：$A \cup (B \cup C) = (A \cup B) \cup C,A \cap (B \cap C) = (A \cap B) \cap C$

• 分配律：$A \cap (B \cup C) = (A \cap B) \cup (A \cap C),A \cup (B \cap C) = (A \cup B) \cap (A \cup C)$

• 德摩根律：$\overline{A \cup B} = \overline{A} \cap \overline{B},\overline{A \cap B} = \overline{A} \cup \overline{B}$

• 吸收律：$A \subset B \Rightarrow A \cup B = B,A \cap B = A$

概率

频率具有不确定性（是一个变量），但是随着试验次数的增加，频率会稳定于一个常数附近。

代数、可测空间、概率空间

对于样本空间 $\Omega$，若 $\mathcal{F}$ 满足：

• $\Omega \in \mathcal{F}$

• $A \in \mathcal{F} \Rightarrow \overline{A} \in \mathcal{F}$

• $A_{1},A_{2},\ldots \in \mathcal{F} \Rightarrow \cup_{n = 1}^{\infty}A_{n} \in \mathcal{F}$

注：若 $\Omega$ 为有限集，则 $\Omega$ 的代数一定为 $\sigma$-代数。

注（勒贝格测度）：TODO

当 $\mathcal{F}$ 为 $\sigma$-代数时，记 $\left( \Omega,\mathcal{F} \right)$ 为可测空间，而对其中的 $\mathcal{F}$ 作为定义域的函数满足概率公理时，记 $\left( \Omega,\mathcal{F},P \right)$ 为概率（测度）空间。

概率的性质

事件 $A$ 出现的概率记为 $P(A)$，满足：

• 非负性：$P(A) \geq 0$

• 规范性：$P(\Omega) = 1$

• 可列可加性：若 $A_{1},A_{2},\ldots$ 两两互不相容，则 $P\left( A_{1} \cup A_{2} \cup \ldots \right) = P\left( A_{1} \right) + P\left( A_{2} \right) + \ldots$

性质有：

• $P(\varnothing) = 0$

• $P(A) = 1 - P\left( \overline{A} \right)$

• 连续性（TODO）

• 多除少补

条件概率、乘法公式、全概率公式、贝叶斯公式

$$P\left( A|B \right) = \frac{P(AB)}{P(B)},P(B) > 0$$

条件概率 $P\left( \cdot ~|~B \right)$ 也是一种概率，满足概率的三个公理。

乘法公式：$P(AB) = P\left( A|B \right)P(B) = P\left( B|A \right)P(A)$

全概率公式：若 $B_{i}$ 为 $\Omega$ 的一个可列划分，则 $P(A) = \sum P\left( A|B_{i} \right)P\left( B_{i} \right)$ （常用于知因求果） 条件全概率公式：$P\left( A|D \right) = \sum P\left( A|B_{i} \cap D \right)P\left( B_{i}|D \right)$

贝叶斯公式：（常用于知果求因）其中 $H_{i}$ 为 $\Omega$ 的一个可列划分$$P\left( H_{i}|E \right) = \frac{P\left( EH_{i} \right)}{P(E)} = \frac{P\left( E|H_{i} \right)P\left( H_{i} \right)}{\sum_{j}P\left( E|H_{j} \right)P\left( H_{j} \right)} = P\left( H_{i} \right)\frac{P\left( E|H_{i} \right)}{\sum_{j}P\left( E|H_{j} \right)P\left( H_{j} \right)}$$ 其中 $P\left( H_{i} \right)$ 被称为先验概率，$P\left( H_{i}|E \right)$ 被称为后验概率，最后的那个分数被称为调整因子。$H$ 代表假设（Hyphothesis），$E$ 代表证据（Evidence）。

独立性

若 $P\left( A|B \right) = P(A) \Leftrightarrow P(AB) = P(A)P(B)$，则称事件 $A$ 和事件 $B$ 相互独立。事件 $A$ 发生的可能性大小不受事件 $B$ 出现与否的影响。

若 $A,B$ 独立，则 $\overline{A},\overline{B},A,B$ 四个事件两两独立。

相互独立：若 $P\left( A_{1}A_{2}\cdots A_{n} \right) = P\left( A_{1} \right)P\left( A_{2} \right)\cdots P\left( A_{n} \right)$，则称事件 $A_{1},A_{2},\cdots,A_{n}$ 相互独立（比两两独立更强）。

$A = \{$ 骰子 1 为奇数 $\}$，$B = \{$ 骰子 2 为奇数 $\}$，$C = \{$ 骰子 1 与 骰子 2 均为奇数 $\}$，则 $A,B,C$ 两两独立，但不相互独立。

随机变量

设 $\left( \Omega,\mathcal{F},P \right)$ 为概率空间

随机变量的定义

$\xi(\omega)$ 是定义在样本空间 $\Omega$ 上的实值函数，若对任意实数 $x$，集合 $$\left\{ \omega:\xi(\omega) \leq x \right\} \in \mathcal{F}$$，则称 $\xi(\omega)$ 为随机变量。$\xi(\omega)$ 将样本点映射到实数上。

记 $\left\{ \xi \leq x \right\} = \left\{ \omega:\xi(\omega) \leq x \right\}$，注意这种记法这是一个样本点的集合。

为什么只要求 $\left\{ \xi \leq x \right\} \in \mathcal{F}$：$\mathcal{F}$ 为 $\sigma$-代数，在此条件满足时，$\left\{ \xi \geq x \right\}$、$\left\{ \xi < x \right\}$、$\left\{ \xi > x \right\}$、$\left\{ \xi = x \right\}$ 等集合也在 $\mathcal{F}$ 中。

随机变量的分布函数

随机变量 $\xi$ 的分布函数 $F(x)$ 定义为 $F(x) = P\left\{ \xi \leq x \right\} = P\left\{ \omega:\xi(\omega) \leq x \right\}$，注意 $\leq$ 符号。

分布函数的性质：

• 单调不减

• 有界性：$0 \leq F(x) \leq 1,F( - \infty) = 0,F( + \infty) = 1$

• 右连续性：$F(x + 0) = F(x)$

若一个函数满足上述三个性质，则一定存在一个随机变量与之对应。

分布律

对于离散型随机变量，其分布函数为分布律，即$P\left( \xi = x_{i} \right) = p_{i}$，其中 $p_{i}$ 为概率，$x_{i}$ 为随机变量 $\xi$ 可能取到的值。

概率密度函数

对于连续型随机变量，其分布函数为概率密度函数，即 $f(x)$，满足 $F(x) = \int_{- \infty}^{x}f(t)dt$。

对于连续型随机变量，分布函数 $F(x)$ 是连续的（左、右连续均满足），还是绝对连续的（即：一致连续、几乎处处可导）。

不可能事件的概率为 $0$，但是概率为 $0$ 的事件不一定是不可能事件。

常见分布

知道：常见分布的数学模型及应用场景
记住：常见分布的分布律、概率密度

概率密度函数的定义域为实数集。为简单起见，下方未定义的区域的概率密度为 $0$。

• 二项分布：$B(n,p)$
  $P(\xi = k) = C_{n}^{k}p^{k}(1 - p)^{n - k},E(\xi) = np,D(\xi) = np(1 - p)$
  来源：$n$ 重伯努利试验中成功次数 $\xi$ 的分布

• 泊松分布：$P(\lambda)$
  $P(\xi = k) = e^{- \lambda}\frac{\lambda^{k}}{k!},E(\xi) = \lambda,D(\xi) = \lambda$
  来源：$B\left( n,\frac{\lambda}{n} \right),n \rightarrow \infty$，即 $\lambda = np_{n}$ 代表了单位时间内事件发生的次数（$p_{n}$ 为将单位时间分为 $n$ 份后，每份内事件发生的概率，这里认为划分后的每份内事件只会发生一次）
  实际问题中, 大量独立重复试验中,“稀有事件”出现的次数可认为服从泊松分布（$n$较大，$p_{n}$较小）

• 几何分布
  $P(\xi = k) = (1 - p)^{k - 1}p$
  来源：第 $k$ 次成功发生的次数 $\xi$ 的分布

• 负二项分布
  $P(\xi = k) = C_{k - 1}^{n - 1}p^{n}(1 - p)^{k - n}$
  来源：第 $n$ 次成功发生的次数 $\xi$ 的分布

• 均匀分布：$U(a,b)$
  $f(x) = \frac{1}{b - a},a \leq x \leq b,E(\xi) = \frac{a + b}{2},D(\xi) = \frac{(b - a)^{2}}{12}$
  

• 指数分布：$E(\lambda),\lambda > 0$
  $f(x) = \lambda e^{- \lambda x},x \geq 0,E(\xi) = \lambda^{- 1},D(\xi) = \lambda^{- 2}\quad(E = \sigma)$
  特点：无后效性（即：$P\left( \xi > s + t~|~\xi > s \right) = P(\xi > t)$）
  来源：泊松过程中两次事件之间的时间间隔（失效率，越高越容易失效）

- 正态分布：$N\left( \mu,\sigma^{2} \right)$
$$f(x) = \frac{1}{\sigma\sqrt{2\pi}}e^{\frac{{- (x - \mu)}^{2}}{2\sigma^{2}}}$$
$N(0,1)$ 称为标准正态分布，其分布函数为 $\Phi(x)$。对于任意正态分布 $N\left( \mu,\sigma^{2} \right)$，其分布函数为 $\Phi(\frac{x - \mu}{\sigma})$

• $\Gamma$ 分布：$\Gamma(\alpha,\beta)$
  $f(x) = \beta^{\alpha}x^{\alpha - 1}\frac{e^{- \beta x}}{\Gamma(\alpha)},x > 0,E(\xi) = \frac{\alpha}{\beta},D(\xi) = \frac{\alpha}{\beta^{2}}$
  $\Gamma(n,1)$ 为 $n$ 阶指数分布，$\Gamma(1,\lambda)$ 为参数为 $\lambda$ 的指数分布
  $\Gamma(1,1)$ 为参数为 $1$ 的指数分布

多维随机变量

如果 $\xi,\eta$ 是定义在同一概率空间 $\left( \Omega,\mathcal{F},P \right)$ 上的两个随机变量，那么称 $(\xi,\eta)$ 为二维随机变量。即一个样本点 $\omega$ 对应两个变量值 $\left( \xi(\omega),\eta(\omega) \right)$。

联合分布函数、边缘分布函数

对于二维随机变量 $(\xi,\eta)$，其联合分布函数 $F(x,y)$ 定义为 $F(x,y) = P\left\{ \xi \leq x,\eta \leq y \right\}$。

对于二维随机变量 $(\xi,\eta)$，其边缘分布函数定义为 $F_{\xi}(x) = P\left\{ \xi \leq x \right\}$ 和 $F_{\eta}(y) = P\left\{ \eta \leq y \right\}$。

联合分布函数可以推导出边缘分布函数，如$F_{\xi}(x) = F(x, + \infty)$。

联合分布函数的性质：

• 单调不减：对一个单独的变量，另一个变量的值增大，概率不会减小。

• 有界性：$0 \leq F(x,y) \leq 1,F( - \infty, \cdot ) = F( \cdot , - \infty) = 0,F( + \infty, + \infty) = 1$

• 右连续性：分别关于单独的变量右连续。

• 相容性：$F\left( x_{2},y_{2} \right) - F\left( x_{1},y_{2} \right) - F\left( x_{2},y_{1} \right) + F\left( x_{1},y_{1} \right) \geq 0$

与一维随机变量类似，若存在一个函数满足上述性质，则一定存在一个二维随机变量与之对应。

二维正态分布

$$(\xi,\eta)\sim N\left( m_{1},\sigma_{1}^{2};m_{2},\sigma_{2}^{2};r \right)$$，其中 $m_{1},m_{2}$ 分别为 $\xi,\eta$ 的均值，$\sigma_{1},\sigma_{2} > 0$ 分别为 $\xi,\eta$ 的标准差，$|r| < 1$ 为相关系数。

若 $(\xi,\eta)\sim N\left( m_{1},\sigma_{1}^{2};m_{2},\sigma_{2}^{2};r \right)$，则 $\xi\sim N\left( m_{1},\sigma_{1}^{2} \right),\eta\sim N\left( m_{2},\sigma_{2}^{2} \right)$。但反之不一定成立。

相互独立性

若 $P\left\{ \xi \leq x,\eta \leq y \right\} = P\left\{ \xi \leq x \right\} P\left\{ \eta \leq y \right\}$，则称 $\xi,\eta$ 相互独立。

等价条件：

• 联合分布函数 $F(x,y) = F_{\xi}(x)F_{\eta}(y)$

• 联合分布律 $p_{ij} = p_{i \cdot}p_{\cdot j}$（若需要否定，则找到一个反例即可）

• 边缘分布函数 $f(x,y) = f_{\xi}(x)f_{\eta}(y)$ 在平面上除去面积为 $0$ 的集合成立

条件分布

对于二维随机变量 $(\xi,\eta)$，若 $F_{\eta}(y) > 0$，则称 $F_{\xi|\eta}\left( x~|~y \right) = P\left\{ \xi \leq x~|~\eta = y \right\} = \frac{F(x,y)}{F_{\eta}(y)}$ 为 $\xi$ 在给定 $\eta = y$ 的条件下的分布函数。

同理，条件概率密度函数 $f_{\xi|\eta}\left( x~|~y \right) = \frac{f(x,y)}{f_{\eta}(y)}$。

独立性：若 $\xi,\eta$ 相互独立，则 $F_{\xi|\eta}\left( x~|~y \right) = F_{\xi}(x)$。

随机变量函数的分布

若 $\xi$ 是随机变量，则对连续函数 $g(\xi)$ 来说也是一个随机变量。

和的分布（记住）

$$f_{X + Y}(z) = F^{\prime}_{X + Y}(z) = \int_{- \infty}^{z}\int_{- \infty}^{+ \infty}f(x,z - x)dxdz = \int_{- \infty}^{+ \infty}f(x,z - x)dx$$

分布函数法

对于 $Y = g(X)$: $$F_{Y}(y) = P\left\{ g(X) \leq y \right\} = \int_{g(x) \leq y}f(x)dx \Rightarrow f_{Y(y)} = F_{Y}^{\prime}(y)$$

随机变量的数字特征

• 期望：随机变量取值的平均值（集中点），记为 $E(\xi)$

• 方差：随机变量取值相对期望的偏离程度，记为 $D(\xi)$

• 相关系数：两个随机变量之间的线性相关程度，记为 $\rho(\xi,\eta)$

期望

$$E(\xi) = \int_{- \infty}^{+ \infty}xdF(x)$$

要求绝对收敛，即 $\int_{- \infty}^{+ \infty}|x|dF(x) < + \infty$。

对于随机变量函数 $Y = g(X)$，$E(Y) = E\left( g(X) \right) = \int_{- \infty}^{+ \infty}g(x)dF(x)$。

TODO：特征函数与矩的关系

公式：

• $E(a\xi + b) = aE(\xi) + b$

• $E\left( \sum a_{i}\xi_{i} \right) = \sum a_{i}E\left( \xi_{i} \right)$

• 相互独立：$E\left( \prod\xi_{i} \right) = \prod E\left( \xi_{i} \right)$

方差与协方差

$$D(\xi) = E\left( \left( \xi - E(\xi) \right)^{2} \right) = E\left( \xi^{2} \right) - \left( E(\xi) \right)^{2}$$

（若 $E\left( \xi^{2} \right)$ 存在，则 $E(\xi)$ 与 $D(\xi)$ 一定存在）

$${Cov}(\xi,\eta) = E\left( \left( \xi - E(\xi) \right)\left( \eta - E(\eta) \right) \right) = E(\xi\eta) - E(\xi)E(\eta)$$

公式：

• $D(a\xi + b) = a^{2}D(\xi),{Cov}(a\xi,b\eta) = ab{Cov}(\xi,\eta)$

• $D(\xi) = {Cov}(\xi,\xi)$

• $D(\xi \pm \eta) = D(\xi) + D(\eta) \pm 2{Cov}(\xi,\eta)$

• ${Cov}(\xi_{1} \pm \xi_{2},\eta) = {Cov}(\xi_{1},\eta) \pm {Cov}(\xi_{2},\eta)$

协方差矩阵 $\Sigma$ 的对角线元素为方差，非对角线元素为协方差；相关系数矩阵同理。

相关系数

$$\rho(\xi,\eta) = \frac{{Cov}(\xi,\eta)}{\sqrt{D(\xi)D(\eta)}} = {Cov}(\xi^{\ast},\eta^{\ast}) \leq 1$$

相关系数是标准化随机变量的协方差。

当 $|\rho| = 1$ 时，两个随机变量完全线性相关，即 $\exists a,b\text{ s.t. }P\left\{ \eta = a + b\xi \right\} = 1$。

当 $\rho = 0$ 时，两个随机变量没有线性相关性（但是可能有非线性相关性，因此不能说明两个随机变量相互独立）。

Chebyshev 不等式

$$P\left\{ |\xi - E(\xi)| \geq \varepsilon \right\} \leq \frac{D(\xi)}{\varepsilon^{2}}$$

方差刻划了随机变量关于其数学期望的偏离程度，随机变量关于其数学期望的偏离程度比关于其它任何值的偏离程度都小！

Cauchy-Schwarz 不等式

$$\left( E(\xi\eta) \right)^{2} \leq E\left( \xi^{2} \right)E\left( \eta^{2} \right)$$

协方差矩阵中，有 $b_{ij}^{2} \leq b_{ii}b_{jj}$。

条件期望、方差

条件数学期望：$E\left( \xi~|~y \right) = E\left( \xi|\eta = y \right) = \int_{- \infty}^{+ \infty}xdF_{\xi|\eta}\left( x~|~y \right)$

若使用 $\eta$ 替换 $y$，则有实值函数 $\delta(y) = E\left( \xi~|~y \right)$。（一般也记 $\mu(x) = E\left( \eta~|~x \right)$），也是随机变量。（如：$E\left( a\xi + b\eta~|~\psi \right) = aE\left( \xi~|~\psi \right) + bE\left( \eta~|~\psi \right)$）

• 若 $\xi,\eta$ 相互独立，则 $E\left( \xi~|~\eta \right) = E(\xi)$

• $E\left( E\left( \xi~|~\eta \right) \right) = E(\xi)$ （全期望公式）

• $E\left( g(\eta)\xi~|~\eta \right) = g(\eta)E\left( \xi~|~\eta \right)$

• $E\left( g(\eta) \cdot \xi \right) = E\left( E\left( g(\eta)\xi~|~\eta \right) \right) = E\left( g(\eta)E\left( \xi~|~\eta \right) \right)$

• $E\left( c|\eta \right) = c$，其中 $c$ 为常数

• $E\left( g(\eta) \right) = E\left( g(\eta) \cdot E\left( 1~|~\psi \right) \right) = E\left( E\left( g(\eta)~|~\psi \right) \right)$

全数学期望公式：$E(\xi) = \int E\left( \xi~|~y \right)dF_{\eta}(y)$

矩

• $n$ 阶原点矩：$E\left( \xi^{n} \right)$，$n$ 阶绝对原点矩：$E\left( |\xi|^{n} \right)$

• $n$ 阶中心矩：$E\left( \left( \xi - E(\xi) \right)^{n} \right)$，$n$ 阶绝对中心矩：$E\left( |\xi - E(\xi)|^{n} \right)$

多维正态随机变量

$$(\xi,\eta)\sim N\left( m_{1},\sigma_{1}^{2};m_{2},\sigma_{2}^{2};r \right)$$

记：

$$E\begin{pmatrix} \xi \\ \eta \end{pmatrix} = \begin{pmatrix} m_{1} & m_{2} \end{pmatrix} = M,\Sigma = \begin{pmatrix} \sigma_{1}^{2} & r\sigma_{1}\sigma_{2} \\ r\sigma_{1}\sigma_{2} & \sigma_{2}^{2} \end{pmatrix}$$

则 $(\xi,\eta)\sim N(M,\Sigma)$

$\left( \xi_{1},\ldots,\xi_{n} \right)$ 服从多维正态分布，则以下命题等价：

• $\xi_{1},\ldots,\xi_{n}$ 相互独立

• $\xi_{1},\ldots,\xi_{n}$ 两两不相关

• $\Sigma$ 为对角矩阵

$\left( \xi_{1},\ldots,\xi_{n} \right)$ 服从 $n$ 维正态分布 $\Leftrightarrow$ 它们的任何非零线性组合服从一维正态分布。

$X = \left( \xi_{1},\ldots,\xi_{n} \right)$ 服从 $n$ 维正态分布，则对于任意矩阵 $A$，$AX\sim N\left( AM,A\Sigma A^{\top} \right)$。

特征函数

$$\varphi(t) = E\left( e^{jt\xi} \right)$$

$$\varphi(t_{1},\ldots,t_{n}) = E\left( e^{j\left( t_{1}\xi_{1} + \ldots + t_{n}\xi_{n} \right)} \right)$$

性质：

• 一致连续、非负定

• $\overline{\varphi(\overset{\rightarrow}{t})} = \varphi( - \overset{\rightarrow}{t})$

• $|\varphi(\overset{\rightarrow}{t})| \leq \varphi(\overset{\rightarrow}{0}) = 1$

• $\varphi(t_{1},0) = \varphi_{\xi}\left( t_{1} \right)$

一致连续、非负定、$\varphi(0) = 1$ 的函数一定是特征函数。

公式：

• $\eta = a\xi + b \Rightarrow \varphi_{\eta}(t) = e^{jbt}\varphi(at)$

• $Z = a\xi + b\eta + c \Rightarrow \varphi_{Z}(t) = e^{jct}\varphi(at,bt)$，特别地，$\varphi_{\xi + \eta}(t) = \varphi(t,t)$

独立性： $\xi_{1},\ldots,\xi_{n}$ 相互独立 $\Leftrightarrow$ $\varphi(t_{1},\ldots,t_{n}) = \varphi_{\xi_{1}}\left( t_{1} \right)\ldots\varphi_{\xi_{n}}\left( t_{n} \right)$（二项分布的来源）

常见特征函数

• 二项分布：$\varphi(t) = \left( 1 - p + pe^{jt} \right)^{n}$

• 泊松分布：$\varphi(t) = \exp(\lambda\left( e^{jt} - 1 \right))$

• 均匀分布：$\varphi(t) = \frac{\sin at}{at},U\lbrack a, - a\rbrack$

• 正态分布：$\varphi(t) = \exp( - \frac{1}{2}t^{2}),N(0,1)$

特征函数与矩

若随机变量 $\xi$ 的 $n$ 阶矩存在,则 $\xi$ 的特征函数的 $k$ 阶导数存在且 $E\left( \xi^{k} \right) = j^{- k}\varphi^{(k)}(0)$。

$D(\xi) = E\left( \xi^{2} \right) - \left( E(\xi) \right)^{2} = - \varphi^{\prime\prime}(0) - \left( \varphi^{\prime}(0) \right)^{2}$

反演公式

唯一性定理：分布函数恒等的充要条件是它们的特征函数恒等。

反演公式： $$F^{\prime}(x) = f(x) = \frac{1}{2\pi}\int_{- \infty}^{+ \infty}e^{- jtx}\varphi(t)dt$$

极限定理

以概率 1 收敛 > 依概率收敛 > 依分布收敛

依分布收敛 / 弱收敛

依分布收敛：对于分布函数列 $\left\{ F_{n}(x) \right\}$，若存在非降函数 $F(x)$ 使得 $$\lim\limits_{n \rightarrow \infty}F_{n}(x) = F(x)$$ 对于 $F(x)$ 的所有连续点成立，则称 $\left\{ F_{n}(x) \right\}$ 依分布收敛于 $F(x)$，记为 $F_{n}(x)\overset{w/L/d}{\longrightarrow}F(x)$。

收敛到的函数 $F(x)$ 不一定是分布函数，如 $F(x) = 0$。

连续性定理

连续性定理可用来确定随机变量序列的极限分布。

正极限定理：若随机变量列 $\left\{ \xi_{n} \right\}$ 依分布收敛于随机变量 $\xi$，则相应的特征函数列 $\left\{ \varphi_{n}(t) \right\}$ 收敛于 $\varphi(t)$，且在 $t$ 的任意有限区间的收敛是一致的。

负极限定理：若特征函数列 $\left\{ \varphi_{n}(t) \right\}$ 收敛于某一函数 $\varphi(t)$，且 $\varphi(t)$ 在 $t = 0$ 处连续，则相应的分布函数列 $\left\{ F_{n}(x) \right\}$ 依分布收敛于某一分布函数 $F(x)$，且其特征函数为 $\varphi(t)$。

依概率收敛

依概率收敛：对于随机变量列 $\left\{ \xi_{n} \right\}$，若对于任意 $\varepsilon > 0$，有 $$\lim\limits_{n \rightarrow \infty}P\left\{ |\xi_{n} - \xi| \geq \varepsilon \right\} = 0$$ 则称 $\left\{ \xi_{n} \right\}$ 依概率收敛于 $\xi$，记为 $\xi_{n}\overset{p}{\rightarrow}\xi$。

$n$ 足够大时，有非常大的把握认为 $\xi_{n}$ 与 $\xi$ 非常接近。

以概率 1 收敛 / 几乎处处收敛

以概率 1 收敛：对于随机变量列 $\left\{ \xi_{n} \right\}$，若 $$P\left( \omega:\lim\limits_{n \rightarrow \infty}\xi_{n}(\omega) = \xi(\omega) \right)$$ ($P\left\{ \lim\limits_{n \rightarrow \infty}\xi_{n} = \xi \right\} = 1$) 则称 $\left\{ \xi_{n} \right\}$ 以概率 1 收敛于 $\xi$，记为 $\xi_{n}\overset{a.s./a.e.}{\longrightarrow}\xi$。

以概率 1 收敛强于依概率收敛：
设 $\Omega = \left\{ \omega_{1},\omega_{2} \right\},P\left\{ \omega_{1} \right\} = P\left\{ \omega_{2} \right\} = \frac{1}{2},\xi(\omega_{1}) = 1,\xi(\omega_{2}) = - 1$。若 $\xi_{n} = - \xi$，则 $\xi_{n}$ 的分布律与 $\xi$ 相同，但 $\xi_{n}$ 与 $\xi$ 不以概率 1 收敛。

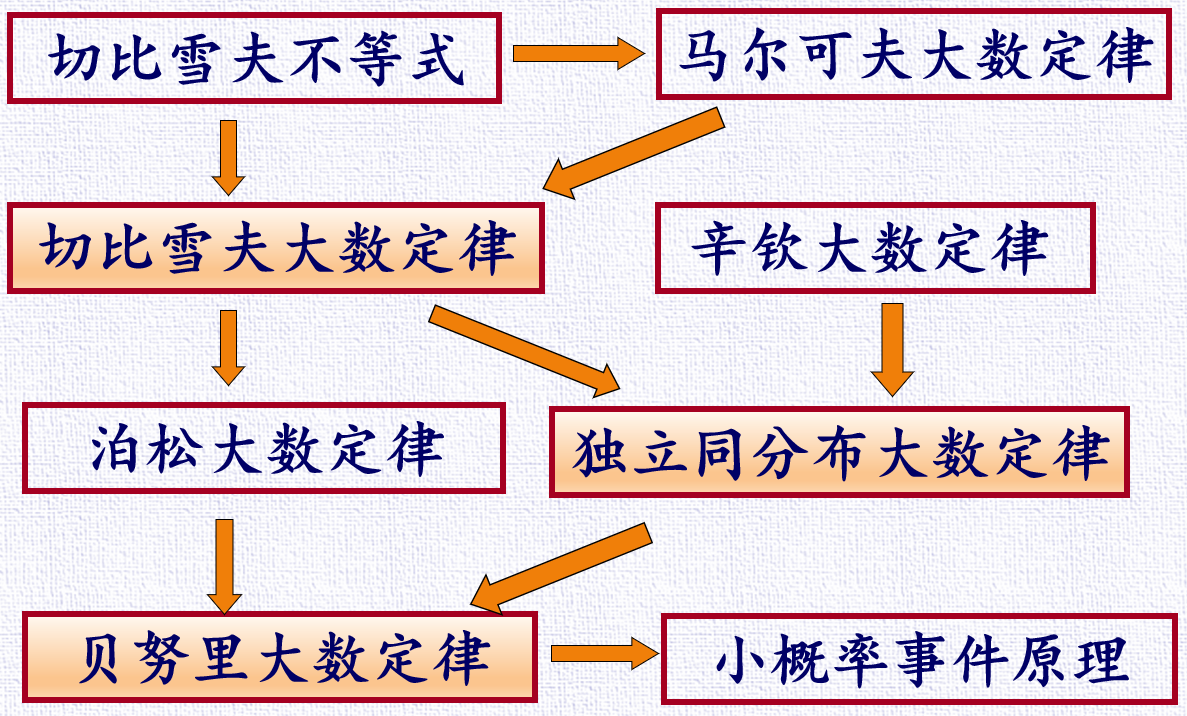
大数定律

弱大数定律

弱大数定律是基于概率收敛的定律。

$$\frac{1}{n}\sum_{i = 1}^{n}\xi_{i} - E(\xi)\overset{p}{\longrightarrow}0$$

1. 贝努利大数定律：$\xi_{1},\xi_{2},\ldots$ 为独立随机变量序列，且 $P\left\{ \xi_{i} = 1 \right\} = p,P\left\{ \xi_{i} = 0 \right\} = 1 - p$（多次独立重复试验的频率紧密地聚集在其概率附近，$p = P(A)$）
   小概率事件原理：概率很小的事件，在一次试验中几乎是不可能发生的，从而在实际中可看成不可能事件

2. 泊松大数定律：$\xi_{1},\xi_{2},\ldots$ 为独立随机变量序列且 $P\left\{ \xi_{i} = 1 \right\} = p_{n},P\left\{ \xi_{i} = 0 \right\} = 1 - p_{n}$

3. 独立同分布大数定律：$\xi_{1},\xi_{2},\ldots$ 为独立同分布随机变量序列，且均值方差存在

4. 切比雪夫大数定律：多个独立，期望存在，方差一致有界的随机变量的算术平均会紧密地聚集在其期望附近。（设 $\xi_{1},\xi_{2},\ldots$ 为期望方差均存在的独立随机变量序列，且方差一致有界，即存在常数 $C$ 使得 $D\left( \xi_{i} \right) \leq C$ ）

5. 马尔可夫大数定律：随机变量序列 $\xi_{1},\xi_{2},\ldots$ （无需独立）满足 $$\lim\limits_{n \rightarrow \infty}\frac{1}{n^{2}}D\left( \sum_{i = 1}^{n}\xi_{i} \right) = 0$$

6. 辛钦大数定律：$\xi_{1},\xi_{2},\ldots$ 为独立同分布随机变量序列，且各自的期望存在

计算定积分：要求 $J = \int_{a}^{b}g(x)dx$，令 $E\left( g(\xi) \right) = \frac{1}{b - a}J$，取独立且服从 $U\lbrack a,b\rbrack$ 的随机变量序列 $\xi_{1},\xi_{2},\ldots$，则 $\frac{1}{n}\sum_{i = 1}^{n}g\left( \xi_{i} \right)\overset{p}{\rightarrow}E\left( g(\xi) \right)$。

用切比雪夫不等式证明切比雪夫大数定律：
$P\left\{ |\frac{1}{n}\sum_{i = 1}^{n}\xi_{i} - \frac{1}{n}\sum_{i = 1}^{n}E\left( \xi_{i} \right)| \geq \varepsilon \right\} \leq \frac{D\left( \frac{1}{n}\sum_{i = 1}^{n}\xi_{i} \right)}{\varepsilon^{2}} = \frac{D\left( \sum_{i = 1}^{n}\xi_{i} \right)}{n^{2}\varepsilon^{2}} \leq \frac{nC}{n^{2}\varepsilon^{2}} \rightarrow 0$

强大数定律

强大数定律是基于几乎处处收敛性的定律。

$$\frac{1}{n}\sum_{i = 1}^{n}\xi_{i} - \frac{1}{n}\sum_{i = 1}^{n}E\left( \xi_{i} \right)\overset{a.s.}{\longrightarrow}0$$

1. 波雷尔大数定律：$\xi_{1},\xi_{2},\ldots$ 为独立同分布随机变量序列，且分布律为 $P\left\{ \xi_{i} = 1 \right\} = p,P\left\{ \xi_{i} = 0 \right\} = 1 - p$ （似乎和贝努利大数定律一样）

2. 科尔莫哥洛夫判别法：$\xi_{1},\xi_{2},\ldots$ 为独立同分布随机变量序列，且 $$\sum_{n = 1}^{\infty}\frac{1}{n^{2}}D\left( \xi_{n} \right) < + \infty$$

3. 科尔莫哥洛夫定理：$\xi_{1},\xi_{2},\ldots$ 为独立同分布随机变量序列，且 $E\left( |\xi_{k}| \right) < + \infty$

中心极限定理

$\xi_{1},\xi_{2},\ldots$ 为独立随机变量序列，且存在有限的期望和方差。若随机变量序列 $$\eta_{n}^{\ast} = \frac{\sum_{i = 1}^{n}\xi_{i} - \sum_{i = 1}^{n}E\left( \xi_{i} \right)}{\sqrt{\sum_{i = 1}^{n}D\left( \xi_{i} \right)}}$$ 对 $z \in {\mathbb{R}}$ 一致地有 $$\lim\limits_{n \rightarrow \infty}P\left\{ \eta_{n}^{\ast} \leq z \right\} = \Phi(z)$$ 则称 $\xi_{1},\xi_{2},\ldots$ 满足中心极限定理。

即：随机变量序列的前 $n$ 项和的标准化随机变量序列依分布收敛于标准正态分布。

独立同分布中心极限定理

$\xi_{1},\xi_{2},\ldots$ 为独立同分布随机变量序列，且 $E\left( \xi_{i} \right) = \mu,D\left( \xi_{i} \right) = \sigma^{2}$，则此随机变量序列满足中心极限定理。

TODO: 林德伯格定理、李雅普诺夫定理

近似计算

若序列 $\xi_{1},\xi_{2},\ldots$ 满足中心极限定理，则对于 $n$ 足够大可以认为 $$\frac{\sum_{i = 1}^{n}\xi_{i} - \sum_{i = 1}^{n}E\left( \xi_{i} \right)}{\sqrt{\sum_{i = 1}^{n}D\left( \xi_{i} \right)}}\sim N(0,1)$$

由两点分布的独立同分布中心极限定理，可以得知当 $n$ 足够大时，二项分布的近似计算可以使用正态分布。一般来说，当 $np > 5,np(1 - p) > 5$ 时，可以使用正态分布进行近似计算。

数理统计

基本概念

• 总体：研究对象的单位元素所组成的集合

• 个体：组成总体的每个单位元素

• 样本：按一定的规则从总体中抽取的部分个体（简单随机样本：相互独立且与总体同分布的样本，简称样本）

• 抽样：从总体中抽取样本的过程

• 统计量：为随机变量且不含未知参数 的 样本的函数，大写

• 统计值：样本值代入统计量中得到的具体数值，小写

• 顺序统计量：样本中的个体按大小排列后的统计量（注意排序破坏了样本间的独立性）
  $\xi_{(k)} = \xi_{(k)}\left( \xi_{1},\xi_{2},\ldots,\xi_{n} \right)$ 满足一个样本观测值中 $x_{(1)} \leq x_{(2)} \leq \ldots \leq x_{(n)}$

总体是随机变量 $\xi$，样本是一组随机变量 $\xi_{1},\xi_{2},\ldots,\xi_{n}$，样本观测值是一组具体数值 $x_{1},x_{2},\ldots,x_{n}$，统计量是样本的函数 $T = T\left( \xi_{1},\xi_{2},\ldots,\xi_{n} \right)$，统计值是样本观测值代入统计量得到的具体数值 $t = T\left( x_{1},x_{2},\ldots,x_{n} \right)$。

常见统计量

• 样本均值：$\overline{\xi} = \frac{1}{n}\sum_{i = 1}^{n}\xi_{i} = A_{1}$

• 样本方差：$S^{2} = \frac{1}{n}\sum_{i = 1}^{n}\left( \xi_{i} - \overline{\xi} \right)^{2} = B_{2}$

• 修正样本方差：$S^{\ast 2} = \frac{1}{n - 1}\sum_{i = 1}^{n}\left( \xi_{i} - \overline{\xi} \right)^{2}$

• 样本 $k$ 阶原点矩：$A_{k} = \frac{1}{n}\sum_{i = 1}^{n}\xi_{i}^{k}$

• 样本 $k$ 阶中心矩：$B_{k} = \frac{1}{n}\sum_{i = 1}^{n}\left( \xi_{i} - \overline{\xi} \right)^{k}$

• 样本协方差：$S_{12} = \frac{1}{n}\sum_{i = 1}^{n}\left( \xi_{i} - \overline{\xi} \right)\left( \eta_{i} - \overline{\eta} \right)$（二维总体 $(\xi,\eta)$ 的样本）

• 样本中位数：$M = \xi_{\left( \frac{n + 1}{2} \right)}$（奇数）或 $\frac{1}{2}\left( \xi_{\left( \frac{n}{2} \right)} + \xi_{\left( \frac{n}{2} + 1 \right)} \right)$（偶数）

• 样本极差：$D_{n}^{\ast} = \xi_{(n)} - \xi_{(1)}$

样本xxx都是随机变量，总体xxx都是常数！

常见统计分布

不会真的有人记得住这些东西的分布律吧……

卡方分布 $\chi^{2}(n)$

设 $\xi_{1},\xi_{2},\ldots,\xi_{n}$ 为 $n$ 个相互独立的标准正态分布随机变量，则 $$\chi^{2} = \sum_{i = 1}^{n}\xi_{i}^{2}\sim\chi^{2}(n)$$ 服从自由度为 $n$ 的卡方分布。

• 数字特征：$\chi^{2}\sim\chi^{2}(n) \longrightarrow E\left( \chi^{2} \right) = n,D\left( \chi^{2} \right) = 2n$

• 可加性：$\eta_{1}\sim\chi^{2}\left( n_{1} \right),\eta_{2}\sim\chi^{2}\left( n_{2} \right)$，则 $\eta_{1} + \eta_{2}\sim\chi^{2}\left( n_{1} + n_{2} \right)$。

• 大样本近似：unimplemented

t 分布 $t(n)$

设 $\xi\sim N(0,1),\eta\sim\chi^{2}(n)$，则 $$T = \frac{\xi}{\sqrt{\eta/n}}\sim t(n)$$ 服从自由度为 $n$ 的 t 分布。

• 关于纵轴对称

• $n$ 较大时，t 分布近似正态分布

F 分布 $F\left( n_{1},n_{2} \right)$

设 $\xi_{1}\sim\chi^{2}\left( n_{1} \right),\xi_{2}\sim\chi^{2}\left( n_{2} \right)$，则 $$F = \frac{\xi_{1}/n_{1}}{\xi_{2}/n_{2}}\sim F\left( n_{1},n_{2} \right)$$ 服从自由度为 $n_{1},n_{2}$ 的 F 分布。

• $F\sim F\left( n_{1},n_{2} \right) \Rightarrow \frac{1}{F}\sim F\left( n_{2},n_{1} \right)$

• $F\sim F\left( n_{1},n_{2} \right) \Rightarrow F_{1 - \alpha}\left( n_{1},n_{2} \right) = \frac{1}{F_{\alpha}\left( n_{2},n_{1} \right)}$

抽样分布定理

单正态总体

$\xi_{1},\xi_{2},\ldots,\xi_{n}$ 为来自总体 $\xi\sim N\left( a,\sigma^{2} \right)$ 的一个样本，$\overline{\xi}$ 为样本均值，$S^{2}$ 为样本方差，则有：

• $\overline{\xi}$ 与 $S^{2}$ 独立

• $\frac{\overline{\xi} - a}{\sigma/\sqrt{n}}\sim N(0,1)$

• $\frac{nS^{2}}{\sigma^{2}}\sim\chi^{2}(n - 1)$

• $\frac{\overline{\xi} - a}{S/\sqrt{n - 1}}\sim t(n - 1)$

双正态总体

总体 $\xi\sim N\left( a_{1},\sigma_{1}^{2} \right),\eta\sim N\left( a_{2},\sigma_{2}^{2} \right)$，样本均值与样本方差分别为 $\overline{\xi},S_{1}^{2}$；$\overline{\eta},S_{2}^{2}$，两总体相互独立。

$$F = \frac{S_{1}^{\ast 2}/\sigma_{1}^{2}}{S_{2}^{\ast 2}/\sigma_{2}^{2}}\sim F\left( n_{1} - 1,n_{2} - 1 \right)$$

当 $\sigma_{1}^{2} = \sigma_{2}^{2} = \sigma^{2}$ 时，$$T = \frac{\left( \overline{\xi} - \overline{\eta} \right) - \left( a_{1} - a_{2} \right)}{S_{w}\sqrt{\frac{1}{n_{1}} + \frac{1}{n_{2}}}}\sim t\left( n_{1} + n_{2} - 2 \right)$$ 其中 $$S_{w}^{2} = \frac{n_{1}S_{1}^{2} + n_{2}S_{2}^{2}}{n_{1} + n_{2} - 2}$$

$\xi + \eta\sim N\left( a_{1} + a_{2},\frac{\sigma^{2}}{n_{1}} + \frac{\sigma^{2}}{n_{2}} \right) \Rightarrow U = \frac{\overline{\xi} + \overline{\eta} - a_{1} - a_{2}}{\sigma\sqrt{\frac{1}{n_{1}} + \frac{1}{n_{2}}}}\sim N(0,1)$

$V = \frac{n_{1}S_{1}^{2}}{\sigma^{2}} + \frac{n_{2}S_{2}^{2}}{\sigma^{2}}\sim\chi^{2}\left( n_{1} + n_{2} - 2 \right)$

参数估计

设总体 $\xi$ 的分布函数为 $F(x;\theta)$，其中 $\theta$ 为未知参数，其取值范围 $\Omega$ 称为参数空间。

点估计

按照一定的优化原则，建立一个统计量 $T$，将其统计值 $t$ 作为参数 $\theta$ 的估计值，$\hat{\theta}$ 称为参数 $\theta$ 的点估计量。

$$\hat{\theta} = T\left( \xi_{1},\xi_{2},\ldots,\xi_{n} \right)$$

矩估计法

用样本矩代替总体矩（如：样本均值代替总体均值，样本方差代替总体方差）。

极大似然估计法

得到观测值后，选取 $\hat{\theta}\left( x_{1},\ldots,x_{n} \right)$ 作为参数 $\theta$ 的估计值，使得当 $\theta$ 取 $\hat{\theta}$ 时，样本观测值出现的概率最大。

似然函数：$$L\left( x_{1},x_{2},\ldots,x_{n};\hat{\theta} \right) = \max\limits_{\theta \in \Omega}L\left( x_{1},x_{2},\ldots,x_{n};\theta \right)$$

一般解法：

1. 构造似然函数

2. 对似然函数取对数

3. 令 $\frac{\partial\ln L}{\partial\theta_{i}} = 0$

并非所有极大似然法都遵循一般步骤（如均匀分布总体的区间端点估计） TODO

估计量的优良性准则

• 无偏性：$E\left( \hat{\theta} \right) = \theta$（渐进无偏性：$\lim\limits_{n \rightarrow \infty}E\left( \hat{\theta} - \theta \right) = 0$）
  修正样本方差 $S^{\ast 2}$ 是无偏估计量，样本方差 $S^{2}$ 是有偏估计量；但在已知总体均值的情况下，$\frac{1}{n}\sum_{i = 1}^{n}\left( \xi_{i} - \mu \right)^{2}$ 是无偏估计量。
  即使 $\hat{\theta}$ 是 $\theta$ 的无偏估计量，$g\left( \hat{\theta} \right)$ 也不一定是 $g(\theta)$ 的无偏估计量。

• 有效性：$D\left( \hat{\theta} \right)$ 尽可能小

• 相合性：估计量随样本容量趋于无穷时依概率（以概率 1）收敛到参数的真实值（样本数量足够大时，估计量稳定于真实值）
  $\lim\limits_{n \rightarrow \infty}P\left\{ |\hat{\theta} - \theta| < \varepsilon \right\} = 1$ （弱相合估计量）
  $P\left\{ \lim\limits_{n \rightarrow \infty}\hat{\theta} = \theta \right\} = 1$ （强相合估计量）

一些估计量：

• 无偏估计量：满足无偏性

• 最小方差无偏估计量：满足无偏性且方差最小（简称最优无偏估计量）

• 最小方差线性无偏估计量：满足无偏性且方差最小且是线性的（是样本的线性函数）

• 最小均方误差估计量：满足均方误差（$E\left( \left( \hat{\theta} - \theta \right)^{2} \right)$）最小

无偏估计量 $\hat{\theta}$ 为 $\theta$ 的最优无偏估计量 $\Leftrightarrow$ 对任何无偏估计量 $T_{0}$ 都有 $E\left( \hat{\theta} \cdot T_{0} \right) = 0$。

结论：若 $\theta$ 为正态总体，则样本均值 $\overline{\xi}$ 是 $\theta$ 的最优无偏估计量，修正样本方差 $S^{\ast 2}$ 是 $\theta$ 的最优无偏估计量。

区间估计，正态总体的枢轴变量法

对于参数 $\theta$，给出一个区间 $\left\lbrack T_{1},T_{2} \right\rbrack$，使得 $P\left\{ \theta \in \left\lbrack T_{1},T_{2} \right\rbrack \right\} = 1 - \alpha$，则称 $\left\lbrack T_{1},T_{2} \right\rbrack$ 为 $\theta$ 的置信区间，$1 - \alpha$ 为置信度（置信水平），$\alpha$ 为显著性水平。

正态总体的枢轴变量法：

1. 选取待估计参数的估计量 $\hat{\theta}$ （原则：优良性准则，常用：$\overline{\xi} \rightarrow \mu,S^{\ast 2} \rightarrow \sigma^{2}$）

2. 构造枢轴变量 $W\left( \xi_{1},\xi_{2},\ldots,\xi_{n};\hat{\theta},\theta \right)$ 且不包含未知参数

3. 使 $W$ 具有经典分布（如：标准正态分布、t 分布、卡方分布、F 分布）

4. 根据置信水平查上侧分位数，使得 $P\left\{ w_{1 - \alpha/2} \leq W \leq w_{\alpha/2} \right\} = 1 - \alpha$

5. 改写得到 $P\left\{ T_{1} \leq \theta \leq T_{2} \right\} = 1 - \alpha$

TODO（！！！）

假设检验

提出统计假设, 根据小概率事件原理用类似反证法的思想对其进行检验。（带有概率性质的反证法）

分布和独立性的假设检验不考

基本概念

• 原假设 $H_{0}$：对总体参数或分布的某种假设，如：$H_{0}:\mu = 114,H_{0}:F(x) = \Phi(x;\mu,\sigma^{2})$

• 备择假设 $H_{1}$：对原假设的否定，如：$H_{1}:\mu \neq 114,H_{1}:H_{1}:\mu = \mu_{1},\ldots$（对于相同的原假设，备择假设可有多种选择）

• 显著性水平 $\alpha$：$H_{0}$ 成立时构造的小概率事件的概率

• 接受域：$H_{0}$ 得以接受时检验统计量的取值范围

• 拒绝域：$H_{0}$ 被拒绝时检验统计量的取值范围

基本步骤

1. 提出原假设 $H_{0}$ 和备择假设 $H_{1}$

2. 建立检验统计量：寻找待检验参数的估计量，并据此建立一个不带未知参数的统计量 $W$

3. 确定 $H_{0}$ 成立时 $W$ 的分布

4. 确定显著性水平 $\alpha$，并根据 $\alpha$ 查找拒绝域

5. 根据样本数据计算 $W$ 的统计值 $w$，并根据 $w$ 是否落在拒绝域中决定是否拒绝 $H_{0}$

如何确定 $\alpha$：当 $\alpha$ 较小时，拒绝域较小，使得 $H_{0}$ 被接受的概率较大，一般对较为信任的原假设取较小的 $\alpha$

有利原则：确定 $H_{0}$ 的拒绝域时，应使得对 $H_{1}$ 成立有利的区域作为拒绝域

两类错误

• 弃真错误：$H_{0}$ 为真，但被拒绝（概率：$\alpha$，显著性水平）

• 纳伪错误：$H_{0}$ 为假，但被接受（概率：$\beta$）

一般先控制弃真错误，再控制纳伪错误

TODO: 检测法

回归分析（概念）

概念

• 相关关系：变量之间存在联系，但无法用确定的函数来明确描述（如：产品的价格Y与需求量X之间存在关系）

• 自变量/可控变量：影响因素，用来解释因变量的变化

• 因变量/被控变量：反映结果，受自变量影响

• 回归函数：$\mu(x_{1},\ldots,x_{n}) = E\left( Y~|~X_{1} = x_{1},\ldots,X_{n} = x_{n} \right)$（是一个确定的函数，可以理解为在 $X = x$ 的条件下 $Y$ 取值的集中点）

  • 基本思想：通过自变量与因变量的观测值，估计回归函数

  • 回归方程：$y = \mu(x_{1},\ldots,x_{n})$

• 回归模型：$Y = \mu(X_{1},\ldots,X_{n}) + \varepsilon$，其中 $\varepsilon$ 为误差项，通常要求：

  1. $E(\varepsilon) = 0$

  2. $D(\varepsilon) = \sigma^{2}$ 尽可能小

• 最小二乘法：使得残差平方和 $Q = \sum\left( y_{i} - \hat{y_{i}} \right)^{2}$ 最小

• 相关系数：$r = \frac{{Cov}(X,Y)}{\sqrt{D(X)D(Y)}}$

• 线性化：将非线性回归模型转化为线性回归模型（例：$y = a\exp(bx) \Rightarrow \ln y = \ln a + bx$）

• 无法线性化：

  • 若可确定回归函数的形式，直接用最小二乘法思想求解其参数估计值

  • 若不可确定回归函数的形式，可考虑用多项式函数近似回归函数，作多项式回归